Problem 4 OMM XII:
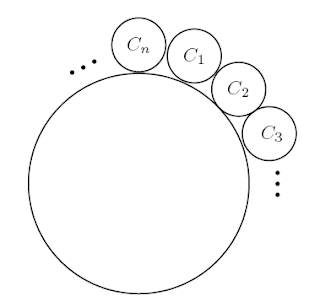
Los caballeros $ C_1,C_2,\ldots,C_n $, del Rey Arturo, se sientan en una mesa
redonda de la siguiente manera:
El rey decide realizar un juego para premiar a uno de sus caballeros. Iniciando con $ C_1 $, y avanzando en el sentido de las manecillas del reloj, los caballeros irán diciendo los números 1, 2, 3, luego 1, 2, 3, y así sucesivamente (cada caballero dice un número). Cada caballero que diga 2 ó 3 se levanta inmediatamente y el juego continúa hasta que queda un solo caballero: el ganador.
Por ejemplo, si $ n = 7 $, los caballeros dirán 1, 2, 3, 1, 2, 3, 1 en la primera vuelta; después $ C_1 $ dirá 2 y $ C_4 $ dirá 3, y gana entonces el caballero $ C_7 $.
Encuentra todos los valores de $ n $ de tal manera que el ganador sea el caballero $ C_{2008} $.
el proximo año intento este y los del año pasado :P
ResponderBorrarcon el próximo año te refieres después de año nuevo o en camino al nacional?
ResponderBorrarMe tarde un buen rato en resolverlo, al menos una hora pero probablemente más como quiera, aqui va la solución:
ResponderBorrarPrimero notemos algunos detalles:
Digamos que tenemos n caballeros y queremos que sobreviva la persona el caballero $k$ la primera ronda. Notemos que para sobrevivir $k \equiv 1 \pmod 3$, de otra manera se muere. Ahora que pasa en la segunda ronda? Una importante deducción es que sobrevivir dos rondas depende de la congruencia de $n$ módulo 3 (y de $k$ por supuesto). Hagamos el analisis para cada congruencia de $n \pmod 3$.
A partir de aquí asumiremos que $k \equiv 1 \pmod 3$ para que sobreviva la primera ronda.
Si $n \equiv 0 \pmod 3$ entonces escribamos $n = 3m$. Notemos que $1,2,3,\ldots,k,\ldots,3m$ se convierte en $1,4,\ldots,k,\ldots,3m-2$. Ahora se empieza a contar de nuevo en $1$ así que podemos imaginarnos que tenemos el juego reducido a $1,2,\ldots, \frac{k+2}{3},\ldots, m$ y querer que sobreviva la ronda $\frac{k+2}{3}$. Para sobrevivir tiene que ser $1$ módulo 3.
Ahora si $n \equiv 1 \pmod 3$, entonces sea $n = 3m + 4$. Hagamos las primeras $2m+2$ eliminaciones tenemos que $1,2,\ldots,k,\ldots,3m+4$ se convierte en $1,4,\ldots,k,\ldots,3m+1,3m+4$, pero ahora $1$ va a contar como $2$ y el $4$ como 3, así que desapareceran, veamos como se ve despues de hacer esos cambios: $7,10,\ldots, k,\ldots, 3m+4$ y ahora si con el 7 siendo el equivalente de $1$. Entonces ahora podemos imaginarnos que tenemos el juego $1,2,\ldots, \frac{k-4}{3},\ldots,m$.
Que pasa con $n \equiv 2 \pmod 3$, escribiendo $n = 3m + 2$, tenemos lo siguient:
$1,2,3,\ldots, k,\ldots,3m+1,3m+2$ se convierte en $1,4,\ldots,k,\ldots,3m+1,3m+2$. Entonces el $3m+2$ es como un 2 y el $1$ es como un 3, entonces podemos borrar esos 2 y nos queda $4,7,10,\ldots,k,\ldots,3m+1$ de manera que el $4$ se cuenta primero. Así que lo transformamos en $1,2,\ldots,\frac{k-1}{3},\ldots,m$.
Ya que hicimos esto vemos que despues de la primera ronda $k$ se convierte en $\frac{k+2}{3}$, $\frac{k-4}{3}$ o $\frac{k-1}{3}$ dependiendo de la congruencia de $n$ módulo 3. Para sobrevivir la siguiente ronda requerimos que esa congruencia sea $1$ módulo 4. Como $\frac{k+2}{3}, \frac{k-4}{3}$ y $\frac{k-1}{3}$ son diferentes módulo 3, sólo una de esas sobrevive la segunda ronda, lo cual nos da información de la congruencia de $n$ módulo $3$ para que $k$ sobreviva dos rondas.
Ahora podemos hacer esto con $k = 2008$ y $n$. Notese que $\frac{k+2}{3},\frac{k-4}{3},\frac{k-1}{3} = 670,668,669$, del cual el $1$ módulo $3$ es $670$ dandonos que $n = 3m$. Ahora usando $k = 670$ y $n = m$, vemos que para sobrevivir tenemos $\frac{k+2}{3},\frac{k-4}{3},\frac{k-1}{3} = 224,222,223$, del cual $223$ es el $1$ módulo $3$ diciendonos que $m = 3m_2 + 2$. Seguiendo este proceso nos vamos de $223$ a $73$ y nos damos cuenta que $m_2 = 3m_3 + 4$, luego de $73$ nos vamos a $25$ y tenemos $m_3 = 3m_4.$ De $25$ nos vamos a $7$ y tenemos que $m_4 = 3m_5 + 4$ y finalmente de $7$ nos vamos a $1$ obteniendo $m_5 = 3m_6 + 4$.
Resolviendo las ecuaciones llegamos a que para sobrevivir 7 rondas necesitamos que $n = 729m_6 + 1338$. Además redujimos el problema a resolver cuando gana el $1$ en un juego con $m_6$ caballeros. Demostraremos que eso pasa sólo cuando $m_6 = 3^l$ ó $m_6 = 2\times 3^l$ para algún $l\geq 0$. Para demostrar eso, notemos que si $m_6 = 1$ o $m_6 = 2$ se cumple que el $1$ gana. Ahora si $m_6 > 2$ y no es múltiplo de 3, entonces usando los mismos argumentos del cuarto párrafo vemos que el $1$ no sobrevive. Por lo tanto cuando $m_6 > 2$ tenemos que $3 | m_6$. Y así podemos seguir dividiendo entre $3$ hasta que lleguemos a $1$ ó $2$ que en tal caso se acaba el problema.Juntando todos los argumentos concluimos que $C_{2008}$ gana sí y sólo sí $n = 2\times 729\times 3^l + 1338$ ó $n = 729 \times 3^l + 1338$ (también lo podemos escribir $n = 2\times3^{l+6}+1338$ ó $n = 3^{l+6}+1338$).