La comunidad de olímpicos, ex-olímpicos, entrenadores y seguidores de la Olimpiada en Chihuahua, wherever they are in the world. Por supuesto cualquier olímpico mexicano (para que parar ahí, de todo el mundo pues), esta invitado a comentar.
viernes, 31 de diciembre de 2010
Problema del Día (31 de Dic)
Sea $P$ un punto fuera del círculo $C$. Considera todos los trapecios inscritos en $C$ tales que sus lados no paralelos se intersectan en $P$ (al prolongarlos). Muestra que las diagonales de dichos trapecios se intersectan todas en un mismo punto (independientemente del trapecio).
jueves, 30 de diciembre de 2010
Problema del Día (30 de Dic)
Hallar todas las funciones $ f: (0,\infty)\mapsto (0,\infty) $ (es decir, las funciones $f$ de los números reales positivos en los números reales positivos) tales que
\[ \frac{\left( f(w)\right)^{2}+\left( f(x)\right)^{2}}{f(y^{2})+f(z^{2}) }=\frac{w^{2}+x^{2}}{y^{2}+z^{2}} \]
para todos los números reales positivos $ w,x,y,z, $ que satisfacen $wx=yz$
\[ \frac{\left( f(w)\right)^{2}+\left( f(x)\right)^{2}}{f(y^{2})+f(z^{2}) }=\frac{w^{2}+x^{2}}{y^{2}+z^{2}} \]
para todos los números reales positivos $ w,x,y,z, $ que satisfacen $wx=yz$
miércoles, 29 de diciembre de 2010
Problema del Día (29 de Dic)
Sea $A$ un subconjunto de $101$ elementos del conjunto $ S=\{1,2,\ldots,1000000\} $. Prueba que existen números $t_1,t_2, \ldots , t_{100}$ en $S$ tales que los conjuntos
\[ A_{j}=\{x+t_{j}\mid x\in A\},\qquad j=1,2,\ldots,100 \]
son disjuntos por parejas.
\[ A_{j}=\{x+t_{j}\mid x\in A\},\qquad j=1,2,\ldots,100 \]
son disjuntos por parejas.
martes, 28 de diciembre de 2010
Problema del día (28 de Dic)
Determina todas las parejas de enteros $(x,y)$ que cumplen:
\[ 1 + 2^x + 2^{2x+1}= y^2\]
\[ 1 + 2^x + 2^{2x+1}= y^2\]
lunes, 27 de diciembre de 2010
Problema del día (27 de Dic)
Otro IMO reciente de geometría.
Sea $ABC$ un triángulo y sea $I$ el centro de su circunferencia inscrita. Sea $P$ un punto en el interior del triángulo tal que
\[ \angle PBA + \angle PCA = \angle PBC + \angle PCB\]
Demuestre que $AP \geq AI$ y que se da la igualdad si y sólo si $P=I$
Sea $ABC$ un triángulo y sea $I$ el centro de su circunferencia inscrita. Sea $P$ un punto en el interior del triángulo tal que
\[ \angle PBA + \angle PCA = \angle PBC + \angle PCB\]
Demuestre que $AP \geq AI$ y que se da la igualdad si y sólo si $P=I$
domingo, 26 de diciembre de 2010
Problema del día (26 de Dic)
Es día de algebra!
Encuentra todas las funciones $f:\mathbb{R}\rightarrow\mathbb{R}$ tales que para todo $x,y\in\mathbb{R}$ se cumple la siguiente igualdad:
\[ f(\left\lfloor x\right\rfloor y)=f(x)\left\lfloor f(y)\right\rfloor \]
Donde $ \left\lfloor a\right\rfloor $ es la función piso.
Este problema es de una IMO reciente, si ya lo habían hecho me dicen para poner otro.
Encuentra todas las funciones $f:\mathbb{R}\rightarrow\mathbb{R}$ tales que para todo $x,y\in\mathbb{R}$ se cumple la siguiente igualdad:
\[ f(\left\lfloor x\right\rfloor y)=f(x)\left\lfloor f(y)\right\rfloor \]
Donde $ \left\lfloor a\right\rfloor $ es la función piso.
Este problema es de una IMO reciente, si ya lo habían hecho me dicen para poner otro.
sábado, 25 de diciembre de 2010
viernes, 24 de diciembre de 2010
Problema del Día (24 Dic)
Regalito adelantado de navidad de combinatoria.
Se tiene un tablero de 100x100. Cada casilla se pinta de uno de $4$ colores distintos de ta manera que en cada fila y cada columna hay exactamente $25$ casillas de cada color. Demuestra que hay $4$ casillas de colores distintos que forman un rectángulo con lados paralelos al tablero.
Se tiene un tablero de 100x100. Cada casilla se pinta de uno de $4$ colores distintos de ta manera que en cada fila y cada columna hay exactamente $25$ casillas de cada color. Demuestra que hay $4$ casillas de colores distintos que forman un rectángulo con lados paralelos al tablero.
jueves, 23 de diciembre de 2010
Problema 4 del nacional XXII (San Carlos 2008)
Este problema es uno de los 4 más difíciles que recuerdo. No me ha salido, otro 4 difícil es el 4 de Oaxtepec 2001 (OMM XV), pero ese me sale cada vez que lo intento porque ya me acuerdo del truquito.
Problem 4 OMM XII:
Los caballeros $ C_1,C_2,\ldots,C_n $, del Rey Arturo, se sientan en una mesa
redonda de la siguiente manera:
El rey decide realizar un juego para premiar a uno de sus caballeros. Iniciando con $ C_1 $, y avanzando en el sentido de las manecillas del reloj, los caballeros irán diciendo los números 1, 2, 3, luego 1, 2, 3, y así sucesivamente (cada caballero dice un número). Cada caballero que diga 2 ó 3 se levanta inmediatamente y el juego continúa hasta que queda un solo caballero: el ganador.
Por ejemplo, si $ n = 7 $, los caballeros dirán 1, 2, 3, 1, 2, 3, 1 en la primera vuelta; después $ C_1 $ dirá 2 y $ C_4 $ dirá 3, y gana entonces el caballero $ C_7 $.
Encuentra todos los valores de $ n $ de tal manera que el ganador sea el caballero $ C_{2008} $.
Problem 4 OMM XII:
Los caballeros $ C_1,C_2,\ldots,C_n $, del Rey Arturo, se sientan en una mesa
redonda de la siguiente manera:
El rey decide realizar un juego para premiar a uno de sus caballeros. Iniciando con $ C_1 $, y avanzando en el sentido de las manecillas del reloj, los caballeros irán diciendo los números 1, 2, 3, luego 1, 2, 3, y así sucesivamente (cada caballero dice un número). Cada caballero que diga 2 ó 3 se levanta inmediatamente y el juego continúa hasta que queda un solo caballero: el ganador.
Por ejemplo, si $ n = 7 $, los caballeros dirán 1, 2, 3, 1, 2, 3, 1 en la primera vuelta; después $ C_1 $ dirá 2 y $ C_4 $ dirá 3, y gana entonces el caballero $ C_7 $.
Encuentra todos los valores de $ n $ de tal manera que el ganador sea el caballero $ C_{2008} $.
Solucion P6 OMM 24
Para los que todavia no saben como se hace el 6 :P
Este es el primer nacional en que se como se hacen los 6 problemas.
Del 2008 no se como hacer el 3,4,5 y del 2009 el 2 y 6
Lo hice ayer en la noche
Esta en un comentario porque esta poco largo.
Este es el primer nacional en que se como se hacen los 6 problemas.
Del 2008 no se como hacer el 3,4,5 y del 2009 el 2 y 6
Lo hice ayer en la noche
Esta en un comentario porque esta poco largo.
Problema del día (23 dic)
Ahora toca números:
Encuentra todas las parejas $(n,m)$ de enteros tales que $2^n+3^m$ es un cuadrado perfecto.
Encuentra todas las parejas $(n,m)$ de enteros tales que $2^n+3^m$ es un cuadrado perfecto.
miércoles, 22 de diciembre de 2010
Problema del Dia (22 Dic)
Vuelve el problema del día al blog. Los problemas que se estarán poniendo serán de nivel avanzado, es decir nacionales dificiles, IMOs faciles y por el estilo.
Los objetivos de esta temporada del problema del día son basicamente apoyar a Karina en su trayecto a la IMO, apoyar a Alberto para que le valla bien en los entrenamientos nacionales y en el proximo nacional y darle algo que hacer a los olimpicos repetidores y entrenadores que se aburren (nos aburrimos) en estas vacaciones de invierno.
Comenzaremos con un problema de geometria de una IMO reciente.
Un triángulo acutángulo $ABC$ tiene ortocentro $H$. La circunferencia con centro en el punto medio de $BC$ que pasa por $H$ corta a la recta $BC$ en $A_1$ y $A_2$. La circunferencia con centro en el punto medio de $CA$ que pasa por $H$ corta a la recta $CA$ en $B_1$ y $B_2$. La circunferencia con centro en el punto medio de $AB$ que pasa por $H$ corta a la recta $AB$ en $C_1$ y $C_2$. Demostrar que $A_1,A_2,B_1,B_2,C_1,C_2$ están sobre una misma circunferencia.
Si a la semana nadie ha resuelto un problema, pongo sugerencia.
Los objetivos de esta temporada del problema del día son basicamente apoyar a Karina en su trayecto a la IMO, apoyar a Alberto para que le valla bien en los entrenamientos nacionales y en el proximo nacional y darle algo que hacer a los olimpicos repetidores y entrenadores que se aburren (nos aburrimos) en estas vacaciones de invierno.
Comenzaremos con un problema de geometria de una IMO reciente.
Un triángulo acutángulo $ABC$ tiene ortocentro $H$. La circunferencia con centro en el punto medio de $BC$ que pasa por $H$ corta a la recta $BC$ en $A_1$ y $A_2$. La circunferencia con centro en el punto medio de $CA$ que pasa por $H$ corta a la recta $CA$ en $B_1$ y $B_2$. La circunferencia con centro en el punto medio de $AB$ que pasa por $H$ corta a la recta $AB$ en $C_1$ y $C_2$. Demostrar que $A_1,A_2,B_1,B_2,C_1,C_2$ están sobre una misma circunferencia.
Si a la semana nadie ha resuelto un problema, pongo sugerencia.
lunes, 20 de diciembre de 2010
Examenes de entrenamiento 1 y 2
PRIMER EXAMEN DE ENTRENAMIENTO
Problema 1.
Muestra que 2010 no se puede escribir como una diferencia de dos cuadrados.
Problema 2.
Sea $ABC$ un triángulo y $D$ un punto sobre el lado $BC$. Sean $U$ el circuncentro del triángulo $BDA$ y $V$ el circuncentro del triangulo $CDA$.
Muestra que $ABC$ y $AUV$ son semejantes.
Problema 3.
Sean $a,b$ numeros reales con $0 \leq a , b \leq 1$. Muestra la desigualdad:
\[ \sqrt{a^3 b^3} + \sqrt{(1-a^2)(1-ab)(1-b^2)} \leq 1 \]
Cuando ocurre la igualdad?
Problema 4.
Una sucesion {$a_n$} con $a_n = a + nd$ se conoce como una $progresion$$aritmetica$. La sucesion {$b_n$} donde $b_n = \sum_{i=0}^{n} a_i$se conoce como una $progresion$$aritmetica$$de$$segundo$$grado$.
Considera todas las progresiones aritmeticas {$a_n$} que cumplan que $a$ y $d$ son enteros positivos y tales que su progresion aritmetica de segundo grado {$b_n$} contiene al numero 2010.
$(a)$ Cual es el mayor indice $n$ que cumple con $b_n = 2010$ ?
$(b)$ Encuentra todas las progresiones aritmeticas {$a_n$} para las que $b_n = 2010$ para el indice $n$ de la parte $(a)$.
SEGUNDO EXAMEN DE ENTRENAMIENTO
Problema 1.
Considera $M_n =$ {$0, 1, 2, \ldots , n$} el conjunto de los enteros no-negativos menores o iguales a $n$. Un subconjunto $K$ de $M_n$ se dira $"regulado"$ si no es vacio y para cada $k \in K$ existe un subconjunto $L$ de $K$ con exactamente $k$ elementos.
Cuantos subconjuntos regulados hay en $M_n$ ?
Problema 2.
Para $n \geq 1$ natural considera a $f(n) = 1 + n + n^2 + \ldots + n^{2010}$ .
Muestra que ningún entero del conjunto {$2, 3, 4, \ldots , 2010$} divide a $f(n)$,
Problema 3.
Una diagonal de un hexagono convexo se dira $"diagonal$$mayor"$, si divide al hexagono en dos cuadrilateros. Dos diagonales mayores dividen al hexagono en dos triangulos y en dos cuadrilateros.
Un hexagono convexo $H$ tiene la propiedad de que cada division de $H$ por dos de sus tres diagonales mayores siempre tiene los dos triangulos isosceles y con lados del hexagono como bases.
Muestra que los vertices de $H$ estan sobre una circunferencia.
Problema 4.
Dos disecciones de un cuadrado en tres rectangulos se consideran iguales si una se puede obtener de la otra por un reacomodo de las tres piezas (para formar el cuadrado).
Cuantas disecciones diferentes hay de un cuadrado de lado 2010 en tres rectangulos, si los rectangulos tienen lados de longitudes enteras y el area de un rectangulo es igual a la media aritmetica de las areas de los otros dos?
Problema 1.
Muestra que 2010 no se puede escribir como una diferencia de dos cuadrados.
Problema 2.
Sea $ABC$ un triángulo y $D$ un punto sobre el lado $BC$. Sean $U$ el circuncentro del triángulo $BDA$ y $V$ el circuncentro del triangulo $CDA$.
Muestra que $ABC$ y $AUV$ son semejantes.
Problema 3.
Sean $a,b$ numeros reales con $0 \leq a , b \leq 1$. Muestra la desigualdad:
\[ \sqrt{a^3 b^3} + \sqrt{(1-a^2)(1-ab)(1-b^2)} \leq 1 \]
Cuando ocurre la igualdad?
Problema 4.
Una sucesion {$a_n$} con $a_n = a + nd$ se conoce como una $progresion$$aritmetica$. La sucesion {$b_n$} donde $b_n = \sum_{i=0}^{n} a_i$se conoce como una $progresion$$aritmetica$$de$$segundo$$grado$.
Considera todas las progresiones aritmeticas {$a_n$} que cumplan que $a$ y $d$ son enteros positivos y tales que su progresion aritmetica de segundo grado {$b_n$} contiene al numero 2010.
$(a)$ Cual es el mayor indice $n$ que cumple con $b_n = 2010$ ?
$(b)$ Encuentra todas las progresiones aritmeticas {$a_n$} para las que $b_n = 2010$ para el indice $n$ de la parte $(a)$.
SEGUNDO EXAMEN DE ENTRENAMIENTO
Problema 1.
Considera $M_n =$ {$0, 1, 2, \ldots , n$} el conjunto de los enteros no-negativos menores o iguales a $n$. Un subconjunto $K$ de $M_n$ se dira $"regulado"$ si no es vacio y para cada $k \in K$ existe un subconjunto $L$ de $K$ con exactamente $k$ elementos.
Cuantos subconjuntos regulados hay en $M_n$ ?
Problema 2.
Para $n \geq 1$ natural considera a $f(n) = 1 + n + n^2 + \ldots + n^{2010}$ .
Muestra que ningún entero del conjunto {$2, 3, 4, \ldots , 2010$} divide a $f(n)$,
Problema 3.
Una diagonal de un hexagono convexo se dira $"diagonal$$mayor"$, si divide al hexagono en dos cuadrilateros. Dos diagonales mayores dividen al hexagono en dos triangulos y en dos cuadrilateros.
Un hexagono convexo $H$ tiene la propiedad de que cada division de $H$ por dos de sus tres diagonales mayores siempre tiene los dos triangulos isosceles y con lados del hexagono como bases.
Muestra que los vertices de $H$ estan sobre una circunferencia.
Problema 4.
Dos disecciones de un cuadrado en tres rectangulos se consideran iguales si una se puede obtener de la otra por un reacomodo de las tres piezas (para formar el cuadrado).
Cuantas disecciones diferentes hay de un cuadrado de lado 2010 en tres rectangulos, si los rectangulos tienen lados de longitudes enteras y el area de un rectangulo es igual a la media aritmetica de las areas de los otros dos?
domingo, 28 de noviembre de 2010
Resultados OMM 24
Estos los resultados de la Olimpiada Mexicana de Matematicas 2010, que se llevó a cabo en Ensenada, Baja California!!
CHIH 1 - Karina - 777744 - 36 - Medalla de Oro!!!
CHIH 2 - Alberto - 717771 - 30 - Medalla de Plata
CHIH 3 - Luis - 313752 - 21 - Medalla de bronce
CHIH 4 - Irving - 351700 - 16 - Medalla de bronce
CHIH 5 - Samantha - 361100 - 11
CHIH 6 - Fabian - 541300 - 13 - Medalla de bronce
Total de puntos 2^7-1
En esta ocasión Chihuahua obtuvo el 5to lugar por estados!!!
Karina quedó preseleccionada para la IMO 2011 en Amsterdam, Paises Bajos y Alberto fue invitado a los entrenamientos nacionales!!
Muchas felicidades a ellos y tambien muchas felicidades a todos los entrenadores!!!
Pongan en los comentarios sus experiencias con este nacional.
CHIH 1 - Karina - 777744 - 36 - Medalla de Oro!!!
CHIH 2 - Alberto - 717771 - 30 - Medalla de Plata
CHIH 3 - Luis - 313752 - 21 - Medalla de bronce
CHIH 4 - Irving - 351700 - 16 - Medalla de bronce
CHIH 5 - Samantha - 361100 - 11
CHIH 6 - Fabian - 541300 - 13 - Medalla de bronce
Total de puntos 2^7-1
En esta ocasión Chihuahua obtuvo el 5to lugar por estados!!!
Karina quedó preseleccionada para la IMO 2011 en Amsterdam, Paises Bajos y Alberto fue invitado a los entrenamientos nacionales!!
Muchas felicidades a ellos y tambien muchas felicidades a todos los entrenadores!!!
Pongan en los comentarios sus experiencias con este nacional.
viernes, 29 de octubre de 2010
Entrenamientos en Juarez
Buenas noches, al parecer el instituto permanecera cerrado asi que el entrenamiento del dia sabado sera cancelado en Ciudad Juarez, en la ciudad de Chihuahua los entrenamientos seguiran normalmente.
Los entrenamientos se reanudan el miercoles a las 4:00 PM en el edificio G.
Saludos
Los entrenamientos se reanudan el miercoles a las 4:00 PM en el edificio G.
Saludos
martes, 26 de octubre de 2010
domingo, 24 de octubre de 2010
Selección CHIHUAHUA 2010
CHIH 1 : Karina Patricia De La Torre Sáenz (CBTIS#128, Cd. Juárez)
CHIH 2 : Aberto Manuel Astizarán Tobin (ITESM, Cd. Juárez)
CHIH 3 : Luis Alonso Ponce Loya (Prepa Chamizal, Cd. Juárez)
CHIH 4 : Irving Martínez Acosta (Radford School, El Paso TX)
CHIH 5 : Samantha Medina Muela (CBTIS#122, Chihuahua)
CHIH 6 : Fabián Rangel Domínguez (COBACH#1, Chihuahua)
Suplente # 1: David Ramírez García
Suplente # 2: María Georgina Gómez Fierro
Por favor esperen todos un correo con las instrucciones de cuales son los pasos a seguir.
lunes, 18 de octubre de 2010
Entrenamientos
Buenas noches a tod@s, para informarles de los proximos entrenamientos que como se han de imaginar son de caracter obligatorio para tod@s, si requieren alguna carta o justificante solo diganme. Los horarios son los siguientes:
Miercoles 20:
Juarez: Edificio G, 16:30 - 20:30 Hrs
Chihuahua: Salon 2305, PrepaTec, 15:00 - 19:00 Hrs
Viernes 22:
Juarez: Edificio G, 16:30 - 20:30 Hrs
Chihuahua: Salon 2305, PrepaTec, 17:00 - 21:00 Hrs
Sabado 23:
Miercoles 20:
Juarez: Edificio G, 16:30 - 20:30 Hrs
Chihuahua: Salon 2305, PrepaTec, 15:00 - 19:00 Hrs
Viernes 22:
Juarez: Edificio G, 16:30 - 20:30 Hrs
Chihuahua: Salon 2305, PrepaTec, 17:00 - 21:00 Hrs
Sabado 23:
Juarez: Edificio G, 10:00 - 14:00 Hrs
Chihuahua: Salon 2305, PrepaTec, 10:00 - 14:00 Hrs
Estan pendientes por definirse entrenamientos de sabado por la tarde, de cualquier manera traten de no hacer planes por si se confirman, el mismo miercoles les damos esta informacion.
Saludos
Problema del día (18 oct)
Sean $a$, $b$ y $c$ enteros positivos tales que: $a$ es impar, el máximo común divisor de $a$, $b$ y $c$ es $1$, y \[\frac{2}{a}+\frac{1}{b}=\frac{1}{c}\]
Prueba que el producto $abc$ es un cuadrado perfecto
domingo, 17 de octubre de 2010
Problema del día (17 oct)
Sea $ABC$ un triángulo isósceles en el que el ángulo $C$ mide
$120$. Una recta por $O$, el circuncentro del triángulo $ABC$, corta a las rectas
$AB$, $BC$ y $CA$ en $X$, $Y$ y $Z$, respectivamente. Demuestra que:
\[\frac{1}{OX} = \frac{1}{OY} + \frac{1}{OZ}\]
sábado, 16 de octubre de 2010
Problema del día. (16 oct)
Sean $a,b,c$ reales positivos que cumplan con
\[\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=1\]
Muestre que
\[a^2+b^2+c^2\geq 2a +2b +2c +9.\]
viernes, 15 de octubre de 2010
Problema del día (15 oct)
Varias canicas de diferentes colores se han distribuido en $25$ cajas. Para cada entero $1 \leq k \leq 25$, cada conjunto de $k$ cajas contiene canicas de exactamente $k+1$ colores diferentes. Muestre que existe un color tal que cada caja contiene una canica de ese color.
Entrenamientos - Semiselección Chihuahua 2010
Nada mas para recordarles que seguimos entrenando como siempre todos los sabados. Todos los ya seleccionados, los que quedan por seleccionar, y los que repiten el año que entra deberán ir.
Cd. Juárez: Edificio G, segundo piso, de 9:00 - 13:00
Chihuahua: Salon 2305, PrepaTec, de 9:00 - 13:00
Saludos
jueves, 14 de octubre de 2010
Resultados Selectivos
Buenos días a tod@s, después de los resultados de los exámenes selectivos, el comité ha decidido que por el momento solo están seleccionad@s a las siguientes personas:
De La Torre Sáenz Karina Patricia |
Astiazarán Tobin Alberto Manuel |
Ponce Loya Luis Alonso |
Quedando 3 lugares pendientes por definirse entre:
Martínez Acosta Irving |
Gómez Fierro María Georgina |
Medina Muela Samantha |
Ramírez García David |
Félix Granados Bryan Adan |
A partir de hoy se estará publicando un problema diario, el cual deberán resolverlo como si se tratara de un problema de selectivo, es decir en papel, con procedimientos y argumentos, deberán escanear estas hojas y mandarlas al correo: selectivos@ommch.org. Estos problemas deberán ser entregados por todos sin excepción, no importa si ya están seleccionados, ya que serán revisados y se llevará a cabo una retroalimentación de todos los detalles del mismo.
Cualquier duda o comentario, pueden enviarme un correo electrónico: esalgado@ommch.org.
Cualquier duda o comentario, pueden enviarme un correo electrónico: esalgado@ommch.org.
domingo, 10 de octubre de 2010
Proceso de revisión
sábado, 9 de octubre de 2010
Tercer selectivo
Hoy es el tercer selectivo, les deseo a tod@s mucho éxito!!, espero que todas las horas de preparación y dedicación les rindan frutos.
Con todo y por todo!!
Saludos.
Con todo y por todo!!
Saludos.
miércoles, 6 de octubre de 2010
Problema del Día (6 de Oct.)
Encontrar todos los enteros positivos $n$ para los cuales $-5^4+5^5+5^n$ es un cuadrado perfecto.
martes, 5 de octubre de 2010
Participación en el Blog
El blog ha tenido muy poca participación.
Un resumen de la participación:
Alberto y Alonso participan en casi todos los problemas. Irving también participa seguido. Bryan tiene un comentario en los últimos 10 días, una buena solución a un problema. Fábian parece tener una solución en el último problema de geometría y Georgina dice que lo solucionó pero no hemos visto la solución.
Si diera calificaciones, Alberto, Irving y Alonso tendrían entre 9 y 10. Bryan, Fabian y Georgina entre 6 y 8 y los demás 0.
Para salir adelante en la olimpiada de matemáticas se tiene que trabajar. Resolver problemas de la olimpiada es algo que requiere de mucha práctica. Los jugadores de fútbol necesitan entrenar varias veces a la semana y estar en buena condición física, nosotros necesitamos que ustedes tengan una buena condición mental. Para ello necesitan intentar el mayor número de problemas que puedan. La idea del blog es darles problemas que puedan intentar en conjunto y de los cuales pueden aprender y usando los comentarios pueden preguntarnos sobre técnicas y sobre las soluciones que otros estudiantes ponen en el blog.
Tienen que echarle ganas. Este fin de semana son los selectivos que decidirán la delegación, ponganle todo el empeño que puedan.
Saludos,
Enrique
Un resumen de la participación:
Alberto y Alonso participan en casi todos los problemas. Irving también participa seguido. Bryan tiene un comentario en los últimos 10 días, una buena solución a un problema. Fábian parece tener una solución en el último problema de geometría y Georgina dice que lo solucionó pero no hemos visto la solución.
Si diera calificaciones, Alberto, Irving y Alonso tendrían entre 9 y 10. Bryan, Fabian y Georgina entre 6 y 8 y los demás 0.
Para salir adelante en la olimpiada de matemáticas se tiene que trabajar. Resolver problemas de la olimpiada es algo que requiere de mucha práctica. Los jugadores de fútbol necesitan entrenar varias veces a la semana y estar en buena condición física, nosotros necesitamos que ustedes tengan una buena condición mental. Para ello necesitan intentar el mayor número de problemas que puedan. La idea del blog es darles problemas que puedan intentar en conjunto y de los cuales pueden aprender y usando los comentarios pueden preguntarnos sobre técnicas y sobre las soluciones que otros estudiantes ponen en el blog.
Tienen que echarle ganas. Este fin de semana son los selectivos que decidirán la delegación, ponganle todo el empeño que puedan.
Saludos,
Enrique
lunes, 4 de octubre de 2010
Problema del día (4 Oct)
Diez niños se sientan en $10$ asientos en hilera. Todos se levantan y vuelven a sentarse usando los $10$ asientos, cada uno sentándose en el asiento en que estaba antes o en un asiento enseguida del que estaba anteriormente. ¿De cuantas maneras pueden volverse a sentar dichos niños?
sábado, 2 de octubre de 2010
Problema del día. (2 oct [no se olvida])
En el triángulo isósceles  , con
, con  ,
,  es un punto sobre la prolongación de
es un punto sobre la prolongación de  tal que
tal que  es perpendicular a
es perpendicular a  ,
,  es un punto sobre la prolongación de
es un punto sobre la prolongación de  tal que
tal que  , y
, y  es un punto sobre
es un punto sobre  tal que
tal que  es paralela a
es paralela a  . Probar que
. Probar que  es paralela a
es paralela a  .
.
 , con
, con  ,
,  es un punto sobre la prolongación de
es un punto sobre la prolongación de  tal que
tal que  es perpendicular a
es perpendicular a  ,
,  es un punto sobre la prolongación de
es un punto sobre la prolongación de  tal que
tal que  , y
, y  es un punto sobre
es un punto sobre  tal que
tal que  es paralela a
es paralela a  . Probar que
. Probar que  es paralela a
es paralela a  .
.
viernes, 1 de octubre de 2010
Guia para registrarse
Como se que van a estar preguntando mucho aqui les va una guia rapida.
1.-Accede https://www.google.com/accounts/Login
2.-Dale click a Create an account now (o el equivalente en español)
3.-Registrate con el correo que usas normalmente
4.-Te va a pedir que pongas un numero de telefono y te va a llegar una llamada donde te dan tu codigo de activacion para verificar que eres humano.
5.-Introduce el codigo
6.- Ve a tu correo y confirma.
7.- Entra a blogger con tu cuenta, te va a pedir nombre.
8.- Ignora lo de crear un blog, y listo ya puedes comentar.
1.-Accede https://www.google.com/accounts/Login
2.-Dale click a Create an account now (o el equivalente en español)
3.-Registrate con el correo que usas normalmente
4.-Te va a pedir que pongas un numero de telefono y te va a llegar una llamada donde te dan tu codigo de activacion para verificar que eres humano.
5.-Introduce el codigo
6.- Ve a tu correo y confirma.
7.- Entra a blogger con tu cuenta, te va a pedir nombre.
8.- Ignora lo de crear un blog, y listo ya puedes comentar.
jueves, 30 de septiembre de 2010
Problema del Día 30 de septiembre
Dados dos enteros positivos $n$ y $a$ se forma una lista de 2001 números como sigue: El primer número es $a$; a partir del segundo, cada número es el residuo que se obtiene al dividir el cuadrado del anterior entre $n$. A los números de la lista se les ponen los signos + y - alternadamente empezando con +. Los números con signo así obtenidos se suman y a esa suma se le llama suma final de $n$ y $a$. ¿Para qué enteros $n\geq 5$ existe alguna $a$ tal que $2 \leq a < \frac{n}{2}$ y la suma final para $n$ y $a$ es positiva?
miércoles, 29 de septiembre de 2010
Problema del dia (29 Sep)
Sea $M$ un conjunto de 10 enteros entre 1 y 100. Probar que dentro de $M$ se pueden encontrar dos subconjuntos ajenos (es decir, sin elementos en común) de tal manera que la suma de los elementos de éstos conjuntos sea la misma.
Sobre los comentarios
Buenas noches a tod@s, solo para avisarles que a raiz de una serie de comentarios, no muy constructivos en las publicaciones de nuestro blog, se ha decidido cerrar el acceso solo a usuarios registrados, es decir, ya no se podra publicar con Anonymous.
Gracias por su comprension.
Gracias por su comprension.
martes, 28 de septiembre de 2010
Problema del dia (27 Sep)
Un cuadrilatero convexo se divide en cuatro triangulos por sus diagonales. Demostrar que el producto de las areas de una pareja de triangulos que tienen solo un vertice en comun es igual al producto de las areas de los otros dos triangulos.
lunes, 27 de septiembre de 2010
2° Entrenamiento General
El 2° entrenamiento general y por lo tanto los selectivos 3 y 4, se llevarán a cabo en el Instituto de Ingeniería y Tecnología de la UACJ del 8 al 10 de Octubre. Les recuerdo que estos selectivos definirán la delegacion Chihuahua 2010.
Horarios:
Viernes 8 de Octubre 4-9 (Entrenamiento)
Sabado 9 de Octubre 9-2 (Examen) 4-9 (Entrenamiento)
Domingo 10 de Octubre 9-2 (Examen)
Saludos
Problemas serios con LaTeX
La página de donde estaba sacando el convertidor de codigo a formulas murió. Estoy tratando de conseguir otra forma de poner LaTeX.
Por lo pronto pongan todo con texto normal.
EDIT:
De vuelta a la normalidad!!!
Por lo pronto pongan todo con texto normal.
EDIT:
De vuelta a la normalidad!!!
domingo, 26 de septiembre de 2010
Problema del dia (26 de Sep)
Se que es muy noche pero aqui va el problema del dia
¿Para cuántas parejas de enteros $(n,r)$ con $0\leq r \leq n \leq 80$ se tiene que $\binom{n}{r} \equiv 2 mod 3$? Calcular la suma módulo 3 de todas las $\binom{n}{r}$ con $0\leq r \leq n \leq 80$.
¿Para cuántas parejas de enteros $(n,r)$ con $0\leq r \leq n \leq 80$ se tiene que $\binom{n}{r} \equiv 2 mod 3$? Calcular la suma módulo 3 de todas las $\binom{n}{r}$ con $0\leq r \leq n \leq 80$.
sábado, 25 de septiembre de 2010
Problema del día. (25 sept)
Dado un número primodemostrar que
no puede ser un cuadrado perfecto.
viernes, 24 de septiembre de 2010
Recordatorio sobre el problema del dia
Las 11 personas que quedan TIENEN que seguir haciendo el problema del día, si nos estamos fijando quien al menos intenta los problemas y quien ni siquiera comenta algo. También quienes ya los intentaron lean los comentarios que les ponemos, parece que muchos de esos comentarios pasan inadvertidos. Los problemas los tienen que seguir intentando hasta que los resuelvan.
Escribo esto porque hay personas entre los 11 preseleccionados que casi no han resuelto problemas y porque en los últimos dos problemas del día ha habido 6 y 3 comentarios, cuando debería haber al menos 11 (al menos 1 por persona).
Problema del dia (24 Sept)
Dados cualesquiera $15$ numeros enteros positivos:
$a_1$, $a_2$, . . . ,$a_{15}$, con $1$ $<$ $a_i \leq 2010$,
que cumplen que cuales quiera dos de ellos son primos relativos.
Demostrar que almenos uno de ellos es primo.
miércoles, 22 de septiembre de 2010
Problema del dia (22 Sep)
Sea $O$ el circuncentro de un triángulo acutángulo $ABC$. Sean $P$ y $Q$ las intersecciones del circuncírculo de AOB con los segmentos $BC$ y $AC$, respectivamente. Sean $N$ la intersección de $PQ$ con la recta $CO$. Muestre que $CN$ es perpendicular a $PQ$.
Entrenamientos - Preselección Chihuahua 2010
Buenas tardes, el entrenamiento del sábado 25 de septiembre se llevará a cabo en las ciudades correspondientes.
Cd. Juárez: Edificio G, segundo piso, de 9:00 - 13:00 y 15:00 - 20:00 hrs.
Chihuahua: Salon 2304, PrepaTec, de 9:00 - 13:00 y 15:00 - 20:00 hrs.
Estos entrenamientos son obligatorios para todos los miembros de la preselección, sin excepción; todos aquellos alumnos que no fueron seleccionados, pero que repitan el año entrante, podrán asistir a todos estos entrenamientos.
Dudas y comentarios: esalgado@ommch.org
Saludos
Preselección Chihuahua
Ya estan los resultados de la primer ronda de selectivos, los alumnos que continuan en el proceso rumbo al nacional son:
De La Torre Sáenz Karina Patricia
Ponce Loya Luis Alonso
Astizarán Tobin Aberto Manuel
Medina Muela Samantha
Ramírez García David
Martínez Acosta Irving
Gómez Fierro María Georgina
Félix Granados Bryan Adan
García Pardo Jesús José
Gutiérrez Sierra Leonardo Isaac
Rangel Domínguez Fabián
Felicidades a todos y recuerden que hay que seguir trabajando en los problemas del blog.
lunes, 20 de septiembre de 2010
Problema del día: 20 Sep
Los divisores positivos del número $24$ son $1, 2, 3, 4, 6, 8, 12, 24$. Su producto es $331776$.
¿Qué se obtiene de multiplicar todos los divisores del número $400$?
P.D. De paso este es el post 200 del blog!!! =)
¿Qué se obtiene de multiplicar todos los divisores del número $400$?
P.D. De paso este es el post 200 del blog!!! =)
Problemas con LaTeX
Ya esta todo bien
domingo, 19 de septiembre de 2010
Problema del 19 de Septiembre
sea $ k_1 k_2 ...k_r $ enteros postitivos tales que $ k_1+k_2+ \cdots +k_r =n $. Demuestra que
$k_1!k_2!\cdots k_r!|n! $
$k_1!k_2!\cdots k_r!|n! $
jueves, 16 de septiembre de 2010
Solución a los Problemas de Calentamiento
Nadie ha resuelto el inciso 1 y 4 y casi todos tienen el mismo error en el inciso 1. En el cuatro parece que casi nadie lo ha intentado. En los incisos 2 y 3 hicieron buen trabajo. Aquí pongo las soluciones:
1) Demostrar que $(a,b) = (a, b-a)$.
Denotemos $d = (a,b)$. Ahora como $d$ es el máximo común divisor entonces $d | a$ y $d | b$. Como $a$ y $b$ son múltiplos de $d$, entonces $b-a$ también es múltiplo de $d$. Lo cual implica que $d | (a,b-a)$. Aquí muchos supusieron que se acaba el problema, sin embargo, no hemos demostrado que no existe algún divisor más grande de $a$ y $b-a$. Denotemos $m = (a,b-a)$. Ahora $a$ es múltiplo de $m$ y $b-a$ es múltiplo de $m$. Por lo tanto $b = a + (b-a)$ también es múltiplo de $m$ (ya que es la suma de dos múltiplos de $m$. Así que $m | (a,b) = d.$ Entonces tenemos que $d | m$ y que $m | d$. La única manera de que $m$ sea múltiplo de $d$ y que $d$ sea múltiplo de $m$ es que $d = m$.
Nota: Algo que hicieron algunos que da otra versión de la solución es escribir $a = dx$ y $b = dy$. Entonces $b-a = d(y-x)$. Ahora como $(a,b) = d$ entonces $(x,y) = 1$. Este hecho que nadie mencionó es bastante útil en problemas de teoría de números.
2) Demuestra que $2^m - 1$ y $2^m + 1$ son primos relativos.
$(2^m - 1,2^m + 1) = (2^m -1, 2^m + 1 - (2^m - 1)) = (2^m - 1, 2) = 1$, ya que $2^m - 1$ es impar y por lo tanto no es divisible entre $2$.
3) Encuentra $(6, 10^{2010})$.
$10^{2010}$ es múltiplo de $2$ pero no de $3$, por lo tanto $(6, 10^{2010}) = 2$.
Nota: Lo que quería que notaran aquí es que sirve ver que pasa con los primos. Lo único que tenían que checar es que pasa con el $2$ y con el $3$ que son los primos que dividen a $6$. También lo pudieron haber solucionado al revés, es decir, analizando los primos que dividen a $10^{2010}$. Por ejemplo, $10^{2010} = 2^{2010} 5^{2010}$, entonces los primos que lo dividen son $2$ y $5$. $6$ es múltiplo de $2$, pero no es múltiplo de $5$, así que $(6, 10^{2010}) = 2$.
Esta idea de ver que pasa con los primos, es muy útil, en particular la pueden usar en el problema del día del 12 de septiembre.
4) Demuestra que si $2^m - 1$ es primo entonces $m$ es primo.
La idea aquí es atacar el problema por contradicción, es decir, asumamos que $2^m - 1$ es primo que $m$ no es primo.
$m$ no es primo, implica que $m = ab$ para algunos $a$ y $b$ donde $a > 1$ y $b > 1$. Entonces
\[2^m - 1 = 2^{ab} - 1 = (2^{a})^{b} - 1 = (2^a - 1)\left((2^a)^{b-1}+(2^a)^{b-2}+\ldots + (2^a)^2 + 2^a + 1\right)\]
Entonces $2^m - 1$ es múltiplo de $2^a - 1$. Como $a > 1$ entonces $2^a - 1$ > 1 y como $a < m$ entonces $2^a - 1 < 2^m - 1$. Por lo tanto $2^m - 1$ no es primo, ya que tiene un divisor que no es 1 o si mismo. Llegamos a una contradicción, empezamos suponiengo que $2^m - 1$ era primo y que $m$ no es primo, pero llegamos a que $2^m - 1$ no es primo. Por lo tanto si $2^m - 1$ es primo, entonces $m$ es primo.
Nota:
En general \[a^n - b^n =(a-b)\left(a^{n-1} + a^{n-2}b + a^{n-3}b^2 + \ldots + a^{2}b^{n-3} + a b^{n-2} + b^{n-1}\right)\]
y en particular poniendo $b = 1$ \[a^n - 1 = (a - 1)\left(a^{n-1} + a^{n-2} + \ldots + a^1 + 1\right)\]
1) Demostrar que $(a,b) = (a, b-a)$.
Denotemos $d = (a,b)$. Ahora como $d$ es el máximo común divisor entonces $d | a$ y $d | b$. Como $a$ y $b$ son múltiplos de $d$, entonces $b-a$ también es múltiplo de $d$. Lo cual implica que $d | (a,b-a)$. Aquí muchos supusieron que se acaba el problema, sin embargo, no hemos demostrado que no existe algún divisor más grande de $a$ y $b-a$. Denotemos $m = (a,b-a)$. Ahora $a$ es múltiplo de $m$ y $b-a$ es múltiplo de $m$. Por lo tanto $b = a + (b-a)$ también es múltiplo de $m$ (ya que es la suma de dos múltiplos de $m$. Así que $m | (a,b) = d.$ Entonces tenemos que $d | m$ y que $m | d$. La única manera de que $m$ sea múltiplo de $d$ y que $d$ sea múltiplo de $m$ es que $d = m$.
Nota: Algo que hicieron algunos que da otra versión de la solución es escribir $a = dx$ y $b = dy$. Entonces $b-a = d(y-x)$. Ahora como $(a,b) = d$ entonces $(x,y) = 1$. Este hecho que nadie mencionó es bastante útil en problemas de teoría de números.
2) Demuestra que $2^m - 1$ y $2^m + 1$ son primos relativos.
$(2^m - 1,2^m + 1) = (2^m -1, 2^m + 1 - (2^m - 1)) = (2^m - 1, 2) = 1$, ya que $2^m - 1$ es impar y por lo tanto no es divisible entre $2$.
3) Encuentra $(6, 10^{2010})$.
$10^{2010}$ es múltiplo de $2$ pero no de $3$, por lo tanto $(6, 10^{2010}) = 2$.
Nota: Lo que quería que notaran aquí es que sirve ver que pasa con los primos. Lo único que tenían que checar es que pasa con el $2$ y con el $3$ que son los primos que dividen a $6$. También lo pudieron haber solucionado al revés, es decir, analizando los primos que dividen a $10^{2010}$. Por ejemplo, $10^{2010} = 2^{2010} 5^{2010}$, entonces los primos que lo dividen son $2$ y $5$. $6$ es múltiplo de $2$, pero no es múltiplo de $5$, así que $(6, 10^{2010}) = 2$.
Esta idea de ver que pasa con los primos, es muy útil, en particular la pueden usar en el problema del día del 12 de septiembre.
4) Demuestra que si $2^m - 1$ es primo entonces $m$ es primo.
La idea aquí es atacar el problema por contradicción, es decir, asumamos que $2^m - 1$ es primo que $m$ no es primo.
$m$ no es primo, implica que $m = ab$ para algunos $a$ y $b$ donde $a > 1$ y $b > 1$. Entonces
\[2^m - 1 = 2^{ab} - 1 = (2^{a})^{b} - 1 = (2^a - 1)\left((2^a)^{b-1}+(2^a)^{b-2}+\ldots + (2^a)^2 + 2^a + 1\right)\]
Entonces $2^m - 1$ es múltiplo de $2^a - 1$. Como $a > 1$ entonces $2^a - 1$ > 1 y como $a < m$ entonces $2^a - 1 < 2^m - 1$. Por lo tanto $2^m - 1$ no es primo, ya que tiene un divisor que no es 1 o si mismo. Llegamos a una contradicción, empezamos suponiengo que $2^m - 1$ era primo y que $m$ no es primo, pero llegamos a que $2^m - 1$ no es primo. Por lo tanto si $2^m - 1$ es primo, entonces $m$ es primo.
Nota:
En general \[a^n - b^n =(a-b)\left(a^{n-1} + a^{n-2}b + a^{n-3}b^2 + \ldots + a^{2}b^{n-3} + a b^{n-2} + b^{n-1}\right)\]
y en particular poniendo $b = 1$ \[a^n - 1 = (a - 1)\left(a^{n-1} + a^{n-2} + \ldots + a^1 + 1\right)\]
lunes, 13 de septiembre de 2010
Problemas de Calentamiento
El problema del día de ayer está un poco difícil. En los comentarios vi que no tenían mucha experiencia con problemas de ese tipo.
Como notación: Para $a$ y $b$ enteros, denota $(a,b)$ al máximo común divisor de $a$ y $b$.
Aquí les van unos problemas para que practiquen:
1) Demuestra que $(a,b) = (a, b-a)$.
2) Calcula el máximo común divisor de $2^m - 1$ y $2^m + 1$.
3) Calcula $(6,10^{2010})$.
4) Demuestra que si $2^m - 1$ es primo, entonces $m$ es primo.
Como notación: Para $a$ y $b$ enteros, denota $(a,b)$ al máximo común divisor de $a$ y $b$.
Aquí les van unos problemas para que practiquen:
1) Demuestra que $(a,b) = (a, b-a)$.
2) Calcula el máximo común divisor de $2^m - 1$ y $2^m + 1$.
3) Calcula $(6,10^{2010})$.
4) Demuestra que si $2^m - 1$ es primo, entonces $m$ es primo.
domingo, 12 de septiembre de 2010
Problema Del Dia 12 de Septiembre
Si m es impar y n es cualquier numero positivo entero. Encuentra el máximo común divisor de $2^m-1$ y $2^n+1$
sábado, 11 de septiembre de 2010
Tarea para el entrenamiento conjunto.
Chavos, aquí les va un problema de TAREA. La veremos en el entrenamiento conjunto. (chavos de Juárez... esta es la tarea que les iba a mandar por mail).
Demuestra que entre cualesquiera 7 enteros existen tres números  tales que
tales que  es múltiplo de $7$.
es múltiplo de $7$.
 tales que
tales que  es múltiplo de $7$.
es múltiplo de $7$.Problema del día. (11 sept)

Sea ABCD un cuadrado con lado 1 cm. Si M y N son los puntos medios de los lados AB y BC, respectivamente. Calcular el área de la zona sombreada.
viernes, 10 de septiembre de 2010
Problema del dia: 10 de Septiembre
A cada vértice de un cubo, se le asigna el numero 1 o el numero -1. Ahora a cada cara se le asigna el producto de los 4 vértices. Cuales son todos los posibles valores de la suma de estos 14 números (hay 6 caras y 8 vértices)?
jueves, 9 de septiembre de 2010
Comentario Extra sobre participación en el blog
Quiero aclarar que los problemas del día los deben seguir intentando hasta que los resuelvan. No porque sea un problema de hace 3 días pueden dejar el problema. Si se rinden y leen otra solución, cerciorense que entiendan esa solución. Traten de aprender algo en cada problema.
La razón por la que escribo esto es que a pesar de haber 37 comentarios en el problema de 1/2*3/4*...*99/100 < 1/raiz(101) no ha habido nadie que lo resuelva. Y el problema no es tan difícil. En los comentarios di una pista y sólo una persona parece haber intentado la pista (aunque nunca nos platicó como le fue en su intento).
La razón por la que escribo esto es que a pesar de haber 37 comentarios en el problema de 1/2*3/4*...*99/100 < 1/raiz(101) no ha habido nadie que lo resuelva. Y el problema no es tan difícil. En los comentarios di una pista y sólo una persona parece haber intentado la pista (aunque nunca nos platicó como le fue en su intento).
Problema del Día 9 de septiembre
Se van escribiendo en orden todos los enteros positivos hasta que entre todas las cifras de los números escritos se hayan usado un millón de unos. ¿Cuál es el último número que se va a escribir?
Por ejemplo, si la condición para terminar fuera usar 5 unos, el último número sería el 12 pues en la lista 1,2,3,4,5,6,7,8,9,10,11,12, se ocupan: un 1 para el 1, uno para el 10, dos para el 11 y uno para el 12. Además ésta es la única respuesta posible pues el siguiente número que se escribiría es 13, que usaría un 1 más.
Por ejemplo, si la condición para terminar fuera usar 5 unos, el último número sería el 12 pues en la lista 1,2,3,4,5,6,7,8,9,10,11,12, se ocupan: un 1 para el 1, uno para el 10, dos para el 11 y uno para el 12. Además ésta es la única respuesta posible pues el siguiente número que se escribiría es 13, que usaría un 1 más.
Participaciones en el blog.
Muchachos, buen día. A partir de hoy, cada semana se hará un análisis de las participaciones en los problemas que se publican, esto con el fin de que identifiquemos (todos) cual es su progreso y esfuerzo.
A continuación verán al lado de sus nombres una serie de números y una igualdad enseguida de ellos. Antes de la igualdad, cada dígito representa la totalidad de participaciones en los problemas del día (desde el 30 de agosto, hasta el 6 de septiembre).
Los criterios son los siguientes:
Problema resuelto: 3pts
Aportación de ideas: 1pt
Ayuda a otra persona: 1pt
No aporta en el comentario: 0pts
Ni siquiera participó: 0pts
Ahora bien, todos los dígitos se suman para dar como resultado el último número. Notemos que hay bastantes 0's, lo que refleja que habrá que ponernos todos a trabajar para elevar la participación y la calidad de las mismas.
Martínez Acosta Irving 33330310=16
Félix Granados Bryan Adan 31303311=15
De La Torre Sáenz Karina Patricia 33030310=13
Ponce Loya Luis Alonso 31330300=13
Ramírez García David 11303311=13
Chávez Soledad Eloy Alfredo 11331310=13
Segovia Guzmán Miguel Omar 11330301=12
Medina Muela Samantha 31310300=11
Pérez Ramírez Neil Alejandro 11301311=11
García Ramos Luis Carlos 11301301=10
Gutiérrez Sierra Leonardo Isaac 30300300=9
García Pardo Jesús José 13110300=9
Sánchez López Luis Rodrigo 10300311=9
Castro Saenz Hugo Valentín 11300300=8
Gómez Fierro María Georgina 00300301=7
Hernández Guerrero Diana Sofía 11300000=5
Escobar Cervantes Erick Eduardo 10300000=4
López Martínez María Carolina 00000301=4
Rangel Domínguez Fabián 00000110=2
Ramírez Luján Jorge Alberto 00000000=0
Flores Ávila Ever Alejandro 00000000=0
EVALUACIÓN DEL TOTAL DEL PUNTAJE:
16 o mas: Excelente
12 a 15: Bueno
8 a 11: Regular
2 a 7: Malo
0 a 1: Preocupante
Hay que trabajar, chavos!!
Un saludo.
miércoles, 8 de septiembre de 2010
Problema del dia (8 sep)
Demostrar que no existe ninguna pareja de primos $p,q$, con $p\textless q$, de tal manera que $p^2 + pq + 6q -1$ sea multiplo de $pq$.
martes, 7 de septiembre de 2010
Problema del Día 7 de septiembre

En un rectángulo de $2\times 3$ se pueden formar 18 rectángulos como pueden ver algunos ejemplos en las figuras. Es fácil notar que en un cuadrado de $2\times 2$ se pueden formar 9 rectángulos. ¿Cuál es el primer $n$ tal que en el cuadrado de $n \times n$ se forman más de 10 000 rectángulos?
lunes, 6 de septiembre de 2010
Problema del dia (6 sep)
Se toma un punto $P$ en el interior de un rectángulo $ABCD$ de tal manera que $\angle APD + \angle BPC = 180^{\circ}$. Encuentra la suma de los ángulos $\angle DAP$ y $\angle BCP$.
domingo, 5 de septiembre de 2010
Problema del dia (5 Sep)
Probar la desigualdad
\[\frac{1}{2}\times \frac{3}{4}\times \frac{5}{6}\times \frac{7}{8}\times \dots \times \frac{99}{100}\textless \frac{1}{\sqrt{101}}\]
\[\frac{1}{2}\times \frac{3}{4}\times \frac{5}{6}\times \frac{7}{8}\times \dots \times \frac{99}{100}\textless \frac{1}{\sqrt{101}}\]
sábado, 4 de septiembre de 2010
Problema del dia (4 Sep)
Cada uno de un grupo de $10$ niños es amigo de exactamente otros $7$ del mismo grupo (la amistad es mutua). Probar que no es posible dividirlos en tres equipos de tal manera que en cada uno de los tres equipos no haya un par de amigos.
viernes, 3 de septiembre de 2010
Problema del dia (3 Sep)
Sea $ABC$ un triángulo acutángulo e isósceles con $AC=AB$. Sean $O$ su circuncentro e $I$ su incentro. Si $D$ es el punto de intersección de $AC$ con la perpendicular a $CI$ que pasa por $O$, demuestra que $ID$ y $AB$ son paralelas.
jueves, 2 de septiembre de 2010
Proximos Entrenamientos y Selectivos 1,2
Aparte de seguir entrenando DIARIO en el blog, los siguientes entrenamientos serán los sábados 4 y 11 de Septiembre de 9AM a 1PM, en Chihuahua coordinado por Isai y en Juárez coordinado por Omar.
ENTRENAMIENTO GENERAL Y SELECTIVOS:
El primer entrenamiento general se llevara a cabo en Ciudad Juárez en el Instituto de Ingeniería de la UACJ en el edificio G del Jueves 16 de Septiembre al Domingo 19 de Septiembre.
La llegada para todos seria el jueves 16 a las 4PM
Jueves 16 Sep: 4-9PM Entrenamiento
Viernes 17 de Sep: 9-2PM y 4-9PM Entrenamiento
Sabado 18 de Sep: 4-9PM Entrenamiento
Sabado 18 de Sep: 9-1:30PM Examen Selectivo #1
Domingo 19 de Sep: 9-1:30PM Examen Selectivo #2
Domingo 19 de Sep: 2PM Salida
Los encargados de los entrenamientos generales serán Héctor y David, el encargado de aplicar los exámenes sera Daniel; Ernesto les mandara cartas a todos para que las entreguen en sus escuelas. Quiero aclarar que no se justifican inasistencias de ningún tipo, especialmente para la gente de Juárez, el hecho de que el entrenamiento vaya a ser en Juárez, no implica que pueden llegar tarde o se pueden salir temprano para ir a clases de ballet o ir a una boda o whatever, si los muchachos de Chihuahua dejan todas sus actividades para estar concentrados esos días en la Olimpiada, es lo mismo que se espera de la gente de Juárez.
Cualquier pregunta en los comentarios.
Saludos
David
ENTRENAMIENTO GENERAL Y SELECTIVOS:
El primer entrenamiento general se llevara a cabo en Ciudad Juárez en el Instituto de Ingeniería de la UACJ en el edificio G del Jueves 16 de Septiembre al Domingo 19 de Septiembre.
La llegada para todos seria el jueves 16 a las 4PM
Jueves 16 Sep: 4-9PM Entrenamiento
Viernes 17 de Sep: 9-2PM y 4-9PM Entrenamiento
Sabado 18 de Sep: 4-9PM Entrenamiento
Sabado 18 de Sep: 9-1:30PM Examen Selectivo #1
Domingo 19 de Sep: 9-1:30PM Examen Selectivo #2
Domingo 19 de Sep: 2PM Salida
Los encargados de los entrenamientos generales serán Héctor y David, el encargado de aplicar los exámenes sera Daniel; Ernesto les mandara cartas a todos para que las entreguen en sus escuelas. Quiero aclarar que no se justifican inasistencias de ningún tipo, especialmente para la gente de Juárez, el hecho de que el entrenamiento vaya a ser en Juárez, no implica que pueden llegar tarde o se pueden salir temprano para ir a clases de ballet o ir a una boda o whatever, si los muchachos de Chihuahua dejan todas sus actividades para estar concentrados esos días en la Olimpiada, es lo mismo que se espera de la gente de Juárez.
Cualquier pregunta en los comentarios.
Saludos
David
Problema del dia (Sep 2)
Encuentra todas las parejas de numeros enteros $(p,q)$ tales que la diferencia entre las dos soluciones de la ecuación $x^2+px+q=0$ sea 2010.
Me alegra la cantidad de respuesta que han recibido estos problemas, sigan asi o mejor. Tambien es buena idea que no solamente hagan los problemas que les ponemos en el blog, ahi tienen folletos con un monton de problemas y si quieren todavia mas problemas solamente avisen.
Me alegra la cantidad de respuesta que han recibido estos problemas, sigan asi o mejor. Tambien es buena idea que no solamente hagan los problemas que les ponemos en el blog, ahi tienen folletos con un monton de problemas y si quieren todavia mas problemas solamente avisen.
miércoles, 1 de septiembre de 2010
Problema del día (Sep 1)
Se tienen $11$ sacos colocados en círculo, cada uno con bolas numeradas en orden del 1 al 11. Se saca la bola $1$ del saco $1$, avanzas $1$, ahora del saco $2$, sacas la pelota con el menor número (el $2$) y avanzas $2$ bolsas, ahora del $4$, sacamos la pelota con el menor número (el $4$), ahora nos movemos $4$, sacamos la bola con el menor número del saco $8$, nos movemos $8$, y así en general, al llegar a un saco sacas la bola con el menor número que quede y procedes a avanzar ese número de veces. Siguiendo este proceso, ¿llegará algún momento en que la bola $2009$ es sacada? Si es así, en cuántos movimientos pasará?
Confirmación de correo.
Muchachos ganadores del estatal:
Se les acaba de enviar un correo de confirmación a las cuentas que registraron en sus cédulas de inscripción. El plan es que respondan precisamente ESE correo haciendo click en RESPONDER A TODOS para que a todos los destinatarios les llegue su confirmación. Hubo algunas cédulas de las cuales no pude comprender del todo la letra, por lo que es incierto que a todos les haya llegado el mensaje. Si no les llegó, por favor notifíquenmelo (dmartinez@ommch.org) con asunto FALLA DE CORREO y diciéndome su nombre.
Un saludo a todos, sigan participando en los problemas que se publiquen, hasta este momento han hecho muy buen trabajo. Felicidades!
martes, 31 de agosto de 2010
Problema del dia (Ago 31)
Demuestra que si en un triangulo de área $S$ el producto de las longitudes de dos de sus medianas es igual a $\frac{3}{2}S$, entonces dichas medianas son perpendiculares.
Si quieren hacer figuras geometricas en la computadora, les recomiendo utilizar GeoGebra.
Si quieren hacer figuras geometricas en la computadora, les recomiendo utilizar GeoGebra.
lunes, 30 de agosto de 2010
Problema del dia (Ago 30)
A partir de este momento se deja de publicar el "Problema del dia para novicios" y ahora pasa a ser solamente "Problema del dia". Estaremos poniendo problemas cada dia, asi como David les dijo despues de la premiación, los preseleccionados estatales deberán mostrar evidencia de que trabajaron en los problemas, ya sea poner la solución completa, poner solo las ideas que resuelven el problema, la forma en que lo estan intentando, dudas acerca de la redaccion, etc. No se fijen en que si alguien ya subió solución del problema o no, ustedes publiquen su solución.
Las soluciones se deben de subir en un comentario, pueden hacerlo en texto normal, en $\LaTeX{}$, a mano y escanearla y poner un link a la imagen, en cualquier documento de office, o cualquier otra forma que se les ocurra.
Y ahora el problema del dia de hoy:
Considera la suma, la diferencia positiva, el producto y el cociente mayor que $1$ de dos enteros positivos distintos. Si al sumar los cuatro resultados obtienes $450$, determina los dos números.
Las soluciones se deben de subir en un comentario, pueden hacerlo en texto normal, en $\LaTeX{}$, a mano y escanearla y poner un link a la imagen, en cualquier documento de office, o cualquier otra forma que se les ocurra.
Y ahora el problema del dia de hoy:
Considera la suma, la diferencia positiva, el producto y el cociente mayor que $1$ de dos enteros positivos distintos. Si al sumar los cuatro resultados obtienes $450$, determina los dos números.
Resultados Examen Estatal 2010
Los siguientes son los ganadores del concurso estatal. Felicidades a tod@s!!!
De La Torre Sáenz Karina Patricia
Astiazarán Tobin Alberto Manuel
Ponce Loya Luis Alonso
Martínez Acosta Irving
Gómez Fierro María Georgina
Medina Muela Samantha
Félix Granados Bryan Adan
Ramírez García David
Gutiérrez Sierra Leonardo Isaac
García Pardo Jesús José
Segovia Guzmán Miguel Omar
Chávez Soledad Eloy Alfredo
Ramírez Luján Jorge Alberto
Escobar Cervantes Erick Eduardo
Flores Ávila Ever Alejandro
Castro Saenz Hugo Valentín
Pérez Ramírez Neil Alejandro
García Ramos Luis Carlos
Sánchez López Luis Rodrigo
Rangel Domínguez Fabián
Hernández Guerrero Diana Sofía
López Martínez María Carolina
De La Torre Sáenz Karina Patricia
Astiazarán Tobin Alberto Manuel
Ponce Loya Luis Alonso
Martínez Acosta Irving
Gómez Fierro María Georgina
Medina Muela Samantha
Félix Granados Bryan Adan
Ramírez García David
Gutiérrez Sierra Leonardo Isaac
García Pardo Jesús José
Segovia Guzmán Miguel Omar
Chávez Soledad Eloy Alfredo
Ramírez Luján Jorge Alberto
Escobar Cervantes Erick Eduardo
Flores Ávila Ever Alejandro
Castro Saenz Hugo Valentín
Pérez Ramírez Neil Alejandro
García Ramos Luis Carlos
Sánchez López Luis Rodrigo
Rangel Domínguez Fabián
Hernández Guerrero Diana Sofía
López Martínez María Carolina
sábado, 28 de agosto de 2010
lunes, 23 de agosto de 2010
Problema del día.
Para novicios:
-Sea $ABC$ un triángulo tal que $AB=AC$ y sea $I$ su incentro. Si $BC=AB+AI$, determina la medida del ángulo $\angle BAC$.
Para avanzados:
-En un congreso internacional se reúnen $n$ científicos de $6$ países. Durante el congreso los científicos se dividen en cuatro secciones de tal manera que dentro de cualquier grupo de $6$ participantes de la misma sección siempre hay dos científicos de la misma edad. Encuentra el mínimo número $n$ para el cual, bajo las condiciones mencionadas arriba, se puede asegurar que existen tres científicos de una misma sección que tienen la misma edad y pertenecen al mismo país.
Para muy avanzados:
-Determina todos los enteros positivos $a$ y $b$ tales que
\[\frac{b^{2}a}{a+b}\]
sea un número primo.
Saludos.
domingo, 22 de agosto de 2010
Foto Reportaje de Karina!
Hey!
Si pueden vean el foto reportaje de Karina (quien tambien participara en el Estatal) en el blog de Gente de la Frontera!
Esta en http://peopleoftheborder.blogspot.com
Saludos a todos.
Nos vemos el proximo sabado en el Estatal!!!! :)
Si pueden vean el foto reportaje de Karina (quien tambien participara en el Estatal) en el blog de Gente de la Frontera!
Esta en http://peopleoftheborder.blogspot.com
Saludos a todos.
Nos vemos el proximo sabado en el Estatal!!!! :)
Problema del dia para novicios
Un paralelogramo $ABCD$ y un triangulo $EBC$ tienen la misma base $BC$ y el vértice $E$ está en la recta que contiene a $AD$. Demuestra que el área del paralelogramo es el doble que el área del triangulo
Publicado por
IwakuraIsa
en
8/22/2010 12:03:00 a.m.
2
comentarios
Etiquetas:
principiante,
problema del dia

martes, 17 de agosto de 2010
Primer entrenamiento para preparatorias. Cd.Juárez
Chavos de prepa: se les invita a participar en la etapa estatal de la Olimpiada Mexicana de Matemáticas en Chihuahua, la cual se llevara a cabo el dia sábado 28 de agosto del presente año.
El primer entrenamiento para ustedes, será este viernes, 20 de agosto, en las instalaciones del IIT (edificio G), ubicado en Av. del Charro, enfrente del Lienzo charro "Adolfo López Mateos" en un horario de 2pm a 6pm.
El siguiente entrenamiento será el sábado 21 de agosto, en el mismo instituto. El día viernes les confirmaremos edificio.
El único material necesario será algún cuaderno para hacer anotaciones, pluma o lapiz y de preferencia juego geometrico (compas, regla).
Los esperamos este viernes!!!
El primer entrenamiento para ustedes, será este viernes, 20 de agosto, en las instalaciones del IIT (edificio G), ubicado en Av. del Charro, enfrente del Lienzo charro "Adolfo López Mateos" en un horario de 2pm a 6pm.
El siguiente entrenamiento será el sábado 21 de agosto, en el mismo instituto. El día viernes les confirmaremos edificio.
El único material necesario será algún cuaderno para hacer anotaciones, pluma o lapiz y de preferencia juego geometrico (compas, regla).
Los esperamos este viernes!!!
Daniel Martínez.
Problemas del dia para novicios
Si creyeron que porque no pusimos problemas en dos dias se escaparon de esos dos dias, pues no es asi jeje.
1. a) Encuentra la mayor potencia de $2$ que divide a $100!$, b) Encuentra la mayor potencia de $2$ que divide a $n!$,
2. Un amigo fue a una fiesta y nos dijo "Fueron $17$ personas y cada una saludó a exactamente $5$ personas". ¿Le crees?
3. Sea $ABCD$ un cuadrilatero cíclico, una circunferencia $\gamma_1$ que pasa por $A$ y $D$ corta a la recta $AB$ en $E$, y otra circunferencia $\gamma_2$ que pasa por $C$ y $D$ corta a la recta $BC$ en $F$. Sea $G$ el segundo punto de intersección de $\gamma_1$ y $\gamma_2$. Muestre que $E$, $F$ y $G$ son colineales.
1. a) Encuentra la mayor potencia de $2$ que divide a $100!$, b) Encuentra la mayor potencia de $2$ que divide a $n!$,
2. Un amigo fue a una fiesta y nos dijo "Fueron $17$ personas y cada una saludó a exactamente $5$ personas". ¿Le crees?
3. Sea $ABCD$ un cuadrilatero cíclico, una circunferencia $\gamma_1$ que pasa por $A$ y $D$ corta a la recta $AB$ en $E$, y otra circunferencia $\gamma_2$ que pasa por $C$ y $D$ corta a la recta $BC$ en $F$. Sea $G$ el segundo punto de intersección de $\gamma_1$ y $\gamma_2$. Muestre que $E$, $F$ y $G$ son colineales.
sábado, 14 de agosto de 2010
Problema del día.
Para novicios:
-Demostrar el criterio de divisibilidad del $11$.
Para avanzados (éste me lo encontré, talvez no sea muy útil, pero si está impresionante):
-In $1647$, Mersenne noted that when a number can be written as a sum of two relatively prime squares in two distinct ways, it is composite and can be factored as follows: if $n=a^2 +b^2 =c^2 +d^2$, then
\[n=\frac{(ac+bd)(ac-bd)}{(a+d)(a-d)}\]
Use this result to factor the numbers
\[493=18^2 +13^2 =22^2 +3^2\]
and
\[38,025=168^2 +99^2 =156^2 +117^2\]
-Demostrar el criterio de divisibilidad del $11$.
Para avanzados (éste me lo encontré, talvez no sea muy útil, pero si está impresionante):
-In $1647$, Mersenne noted that when a number can be written as a sum of two relatively prime squares in two distinct ways, it is composite and can be factored as follows: if $n=a^2 +b^2 =c^2 +d^2$, then
\[n=\frac{(ac+bd)(ac-bd)}{(a+d)(a-d)}\]
Use this result to factor the numbers
\[493=18^2 +13^2 =22^2 +3^2\]
and
\[38,025=168^2 +99^2 =156^2 +117^2\]
viernes, 13 de agosto de 2010
Problema del dia para novicios
Se tienen $n+1$ elementos del conjunto \[ \{1,2, \dots ,2n \} \]
a) Demostrar que entre esos $n+1$ elementos siempre hay dos consecutivos.
b) Demostrar que hay dos de esos elementos tales que uno divide al otro
a) Demostrar que entre esos $n+1$ elementos siempre hay dos consecutivos.
b) Demostrar que hay dos de esos elementos tales que uno divide al otro
jueves, 12 de agosto de 2010
Problema del dia
para novicios:
Demostrar que si $p$ es primo y $p^2+2$ es primo, entonces $p^3+2$ es primo
Demostrar que si $p$ es primo y $p^2+2$ es primo, entonces $p^3+2$ es primo
miércoles, 11 de agosto de 2010
Problema del día
Problema para novicios:
Sea ABC un triangulo. La bisectrices de los angulos en A, B y C intersectan al circuncirculo del triangulo ABC en los puntos K, L, M respectivamente. Demostrar que LM es perpendicular a AK.
Problema para avanzados:
Sea $\gamma$ una circunferencia de centro O y sea A un punto fuera de ella. Las tangentes a $\gamma$ que pasan por A tocan a $\gamma$ en los puntos B y C. Sea D el punto donde intersecta la recta OA con $\gamma$. Sea X el pie de la perpendicular de B hacia DC y llamemos Y al punto al punto medio de XB. La recta DY corta por segunda vez a $\gamma$ en un punto Z. Demostrar que CZ es perpendicular a AZ.
Saludos.
Manuel.
Sea ABC un triangulo. La bisectrices de los angulos en A, B y C intersectan al circuncirculo del triangulo ABC en los puntos K, L, M respectivamente. Demostrar que LM es perpendicular a AK.
Problema para avanzados:
Sea $\gamma$ una circunferencia de centro O y sea A un punto fuera de ella. Las tangentes a $\gamma$ que pasan por A tocan a $\gamma$ en los puntos B y C. Sea D el punto donde intersecta la recta OA con $\gamma$. Sea X el pie de la perpendicular de B hacia DC y llamemos Y al punto al punto medio de XB. La recta DY corta por segunda vez a $\gamma$ en un punto Z. Demostrar que CZ es perpendicular a AZ.
Saludos.
Manuel.
martes, 10 de agosto de 2010
Problema del día.
Problema para novicios:
-Probar que si $a$ y $b$ son enteros impares, entonces $16|a^4+b^4-2$
Problema para avanzados: (no se que tan facil este)
-Sea $t_n$ el $n-esimo$ número triangular $\left(t_{n}=\frac{n(n+1)}{2}\right)$. Encontrar todos los valores de $n$ para los cuales $t_n$ divide a
\[\sum_{i=1}^{n} t_i\]
-Probar que si $a$ y $b$ son enteros impares, entonces $16|a^4+b^4-2$
Problema para avanzados: (no se que tan facil este)
-Sea $t_n$ el $n-esimo$ número triangular $\left(t_{n}=\frac{n(n+1)}{2}\right)$. Encontrar todos los valores de $n$ para los cuales $t_n$ divide a
\[\sum_{i=1}^{n} t_i\]
sábado, 7 de agosto de 2010
Problema del dia para novicios
$x,y,z$ son reales positivos, diferentes entre si que cumplen:
\[\frac{y}{x-z}=\frac{x+y}{z}=\frac{x}{y}\]
¿Cuanto vale $$\frac{x}{y}$$?
\[\frac{y}{x-z}=\frac{x+y}{z}=\frac{x}{y}\]
¿Cuanto vale $$\frac{x}{y}$$?
viernes, 6 de agosto de 2010
Problema del dia para novicios
Demuestra que las diagonales de un paralelogramo se cortan en sus puntos medios.
jueves, 5 de agosto de 2010
Problema del día.
Problema para novicios:
-Demostrar que si $a$ es impar, entonces $32|(a^2 +7)(a^2 +3)$
-Demostrar que si $a$ es impar, entonces $32|(a^2 +7)(a^2 +3)$
miércoles, 4 de agosto de 2010
Problema del día.
Problema para novicios:
-Dada una lista de $0$'s y $1$'s le podemos aplicar la operación siguiente: Se escogen dos números $a$ y $b$ de la lista, se borran y se agrega a la lista el número $0$ si $a=b$, y $1$ si $a$ es distinto de $b$. Se repite esta operación hasta quedarse con un solo número. Determinar cómo debe ser la lista para terminar con un $1$.
Este problema lo encontré asi de volada.. por eso no puse para los chavos avanzados.
-Dada una lista de $0$'s y $1$'s le podemos aplicar la operación siguiente: Se escogen dos números $a$ y $b$ de la lista, se borran y se agrega a la lista el número $0$ si $a=b$, y $1$ si $a$ es distinto de $b$. Se repite esta operación hasta quedarse con un solo número. Determinar cómo debe ser la lista para terminar con un $1$.
Este problema lo encontré asi de volada.. por eso no puse para los chavos avanzados.
lunes, 2 de agosto de 2010
Problemas del dia
Como ayer no pusimos problema, ahora pondremos 2 de cada tipo
Novicios:
Demostrar que los puntos medios de los lados de un cuadrilatero cualquiera son los vertices de un paralelogramo.
Determinar todos los primos p para los cuales $p^2+77$ tiene exactamente $5$ divisores.
Avanzado:
Por el baricentro $G$ de un triangulo $ABC$ se traza una recta que corta al lado $AB$ en $P$ y al lado $AC$ en $Q$. Demuestra que
\[\frac{PB}{PA}\cdot \frac{QC}{QA} \leq \frac{1}{4} \]
Probar que para todo numero natural $n$, el número
\[(n^3-n)(5^{8n+4}+3^{4n+2})\]
es multiplo de 3804
Novicios:
Demostrar que los puntos medios de los lados de un cuadrilatero cualquiera son los vertices de un paralelogramo.
Determinar todos los primos p para los cuales $p^2+77$ tiene exactamente $5$ divisores.
Avanzado:
Por el baricentro $G$ de un triangulo $ABC$ se traza una recta que corta al lado $AB$ en $P$ y al lado $AC$ en $Q$. Demuestra que
\[\frac{PB}{PA}\cdot \frac{QC}{QA} \leq \frac{1}{4} \]
Probar que para todo numero natural $n$, el número
\[(n^3-n)(5^{8n+4}+3^{4n+2})\]
es multiplo de 3804
sábado, 31 de julio de 2010
Problema del día.
Problema del día para novicios:
-A un tablero cuadriculado de 9 x 9 se le han quitado tres de sus esquinas (de 1x1). ¿Es posible cubrirlo con fichas de 3x1?
Para avanzados:
-La sucesión de Fibonacci $f_1 , f_2 , ... $ se define como sigue: $f_1 =1$, $f_2 =1$ y, para $n \geq 3$, $f_n = f_{n-1} + f_{n-2}$. Probar la siguiente fórmula:
\[f_n = \frac{\left(\frac{1+\sqrt{5}}{2}\right)^n - \left(\frac{1-\sqrt{5}}{2}\right)^n}{\sqrt{5}}\]
-A un tablero cuadriculado de 9 x 9 se le han quitado tres de sus esquinas (de 1x1). ¿Es posible cubrirlo con fichas de 3x1?
Para avanzados:
-La sucesión de Fibonacci $f_1 , f_2 , ... $ se define como sigue: $f_1 =1$, $f_2 =1$ y, para $n \geq 3$, $f_n = f_{n-1} + f_{n-2}$. Probar la siguiente fórmula:
\[f_n = \frac{\left(\frac{1+\sqrt{5}}{2}\right)^n - \left(\frac{1-\sqrt{5}}{2}\right)^n}{\sqrt{5}}\]
viernes, 30 de julio de 2010
Guia para usar LaTeX
Para poner un codigo en LaTeX basta ponerlo entre signos de $, si lo pones entre doble signo de $ saldra en linea pero con letra mas grande y para ponerlo grande y centrado hay que ponerlo asi hay que usar $\backslash [ codigolatex \backslash]$
Aqui hay una guia en otro sitio que esta muy buena http://www.matetam.com/de-consulta/acordeones/latex
Si ves alguna expresión matemática en este blog y quieres saber como se escribió, solo basta poner el cursor encima de la expresión matemática y saldrá el código LaTeX que se usó para esa formula.
Aqui un ejemplo:
\[x=\frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\]
Es la formula general para las ecuaciones cuadráticas, es decir de la forma $ax^2+bx+c=0$
Pueden hacer experimentos con los comentarios de este post.
Ademas aqui esta una pagina con mas ejemplos:
http://www.watchmath.blogspot.com/
Aqui hay una guia en otro sitio que esta muy buena http://www.matetam.com/de-consulta/acordeones/latex
Si ves alguna expresión matemática en este blog y quieres saber como se escribió, solo basta poner el cursor encima de la expresión matemática y saldrá el código LaTeX que se usó para esa formula.
Aqui un ejemplo:
\[x=\frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\]
Es la formula general para las ecuaciones cuadráticas, es decir de la forma $ax^2+bx+c=0$
Pueden hacer experimentos con los comentarios de este post.
Ademas aqui esta una pagina con mas ejemplos:
http://www.watchmath.blogspot.com/
Problema del día
Para novicios:
Si $a$ y $b$ son numeros positivos distintos que cumplen $a^2+b^2=4ab$, hallar el valor de: \[\frac{a+b}{a-b}\]
Avanzados:
Sean $a,b,c>0$ muestre que
\[\frac{a^2+b^2}{a+b}+\frac{b^2+c^2}{b+c}+\frac{a^2+c^2}{a+c}\geq a+b+c\]
Muy avanzado:
Sean $a,b,c$ números reales positivos con $abc=1$. Muestre que:
\[\left(a-1+\frac{1}{b}\right)\left(b-1+\frac{1}{c}\right)\left(c-1+\frac{1}{a}\right)\leq1\]
Si $a$ y $b$ son numeros positivos distintos que cumplen $a^2+b^2=4ab$, hallar el valor de: \[\frac{a+b}{a-b}\]
Avanzados:
Sean $a,b,c>0$ muestre que
\[\frac{a^2+b^2}{a+b}+\frac{b^2+c^2}{b+c}+\frac{a^2+c^2}{a+c}\geq a+b+c\]
Muy avanzado:
Sean $a,b,c$ números reales positivos con $abc=1$. Muestre que:
\[\left(a-1+\frac{1}{b}\right)\left(b-1+\frac{1}{c}\right)\left(c-1+\frac{1}{a}\right)\leq1\]
jueves, 29 de julio de 2010
Problema del día.
Para seleccionados regionales:
-En la siguiente progresión aritmética: $t_1 , t_2 ,..., t_{47}$, la suma de los términos impares es $$1272$$. ¿Cuál es la suma de los $$47$$ términos?
Para avanzados:
-Si las soluciones a, b y c de la ecuación $$x^3-2x^2-5x+6=0$$ son distintas de cero, ¿cuál es el valor de:
\[\frac{1}{ab} + \frac{1}{ac} + \frac{1}{bc}\]?
Les debo el de "muy avanzados" (entrenadores)... se los publico por la tarde.
Edit de Isai:
Ya tenemos $$\LaTeX{}$$ en el blog!!!!
Edit 2 de Isai:
Y hasta funciona en los comentarios!!!!!!
-En la siguiente progresión aritmética: $t_1 , t_2 ,..., t_{47}$, la suma de los términos impares es $$1272$$. ¿Cuál es la suma de los $$47$$ términos?
Para avanzados:
-Si las soluciones a, b y c de la ecuación $$x^3-2x^2-5x+6=0$$ son distintas de cero, ¿cuál es el valor de:
\[\frac{1}{ab} + \frac{1}{ac} + \frac{1}{bc}\]?
Les debo el de "muy avanzados" (entrenadores)... se los publico por la tarde.
Edit de Isai:
Ya tenemos $$\LaTeX{}$$ en el blog!!!!
Edit 2 de Isai:
Y hasta funciona en los comentarios!!!!!!
miércoles, 28 de julio de 2010
Problema del día para novicios
Para calentar:
Demostrar que al trazar la diagonal en un paralelogramo se forman dos triangulos congruentes.
El de verdad:
Sean $E,F,K,L$ puntos sobre los lados $AB,BC,CD$ y $DA$ del cuadrado $ABCD$,respectivamente. Muestre que si los segmentos $EK$ y $FL$ son perpendiculares entonces $EK=FL$.
Demostrar que al trazar la diagonal en un paralelogramo se forman dos triangulos congruentes.
El de verdad:
Sean $E,F,K,L$ puntos sobre los lados $AB,BC,CD$ y $DA$ del cuadrado $ABCD$,respectivamente. Muestre que si los segmentos $EK$ y $FL$ son perpendiculares entonces $EK=FL$.
Publicado por
IwakuraIsa
en
7/28/2010 07:44:00 p.m.
0
comentarios
Etiquetas:
principiante,
problema del dia

martes, 27 de julio de 2010
Problema del día para novicios.
1-¿Cuántas diagonales tiene un polígono de n lados (convexo)?
2-¿Cuántos divisores positivos tiene el número 2009?
3-Los Rotokas de Papua Nueva Guinea tienen un alfabeto compuesto por 11 letras: A, B, E, G, I, K, O, P, R, T y U. Si las placas de los coches tienen sólo 5 letras diferentes entre si, ¿cuántas placas se pueden formar con este alfabeto que empiecen con G o K y terminen con T?
Se les proponen tres problemas porque son todos de solución rápida, aún con este argumento, sus soluciones tienen ideas importantes que se rescatarán dentro de los entrenamientos.
Saludos.
2-¿Cuántos divisores positivos tiene el número 2009?
3-Los Rotokas de Papua Nueva Guinea tienen un alfabeto compuesto por 11 letras: A, B, E, G, I, K, O, P, R, T y U. Si las placas de los coches tienen sólo 5 letras diferentes entre si, ¿cuántas placas se pueden formar con este alfabeto que empiecen con G o K y terminen con T?
Se les proponen tres problemas porque son todos de solución rápida, aún con este argumento, sus soluciones tienen ideas importantes que se rescatarán dentro de los entrenamientos.
Saludos.
Daniel.
Publicado por
el colado
en
7/27/2010 01:58:00 a.m.
9
comentarios
Etiquetas:
principiante,
problema del dia

Próximos entrenamientos. Cd. Juárez.
A los muchachos de ciudad Juárez que quedaron seleccionados para participar en la olimpiada estatal, se les notifican los horarios para los proximos entrenamientos:
J u l i o :
jueves 29: de 2pm a 6pm.
viernes 30: de 2pm a 6pm.
sábado 31: de 9am a 1pm.
A g o s t o :
Viernes 6, 13 y 20: de 2pm a 6pm.
Sábados 7, 14 y 21: de 9 a 1pm
En total serán nueve entrenamientos antes del concurso estatal en los cuales la asistencia ES OBLIGATORIA. Si por algún motivo (que deberán explicar) no pueden asistir, sólo tienen que cubrir una tarea que les mandaremos por correo electrónico. Tratará de una selección de problemas que aumentarán de nivel conforme al número de inasistencias; todo se los explicaremos más a detalle en el primer entrenamiento, por lo que es de suma importancia que asistan.
Las sesiones serán en el segundo piso del edificio G del IIT (donde hicieron el examen).
A los chavos de prepa, se les recuerda que su primer entrenamiento será el día sábado 14 de agosto, edificio G de 9am a 1pm. El siguiente será el 21 con el mismo horario. Las instalaciones serán las mismas que para los de secundaria.
nota: los chavos que acaban de pasar a prepa que quedaron seleccionados deberán asistir a los entrenamientos mencionados al principio.
Saludos!... Éxito!!
J u l i o :
jueves 29: de 2pm a 6pm.
viernes 30: de 2pm a 6pm.
sábado 31: de 9am a 1pm.
A g o s t o :
Viernes 6, 13 y 20: de 2pm a 6pm.
Sábados 7, 14 y 21: de 9 a 1pm
En total serán nueve entrenamientos antes del concurso estatal en los cuales la asistencia ES OBLIGATORIA. Si por algún motivo (que deberán explicar) no pueden asistir, sólo tienen que cubrir una tarea que les mandaremos por correo electrónico. Tratará de una selección de problemas que aumentarán de nivel conforme al número de inasistencias; todo se los explicaremos más a detalle en el primer entrenamiento, por lo que es de suma importancia que asistan.
Las sesiones serán en el segundo piso del edificio G del IIT (donde hicieron el examen).
A los chavos de prepa, se les recuerda que su primer entrenamiento será el día sábado 14 de agosto, edificio G de 9am a 1pm. El siguiente será el 21 con el mismo horario. Las instalaciones serán las mismas que para los de secundaria.
nota: los chavos que acaban de pasar a prepa que quedaron seleccionados deberán asistir a los entrenamientos mencionados al principio.
Saludos!... Éxito!!
Daniel
RECUERDEN QUE TIENEN TAREA (los problemas para novicios)
sigan siendo felices.... ☺
sábado, 24 de julio de 2010
Problema del día.
Para seleccionados regionales:
-Encuentra un número de dos dígitos tal que al sumarle 1 y voltear los dígitos del resultado, obtienes un divisor del número.
Para avanzados:
-Encontrar todas las parejas de cuadrados perfectos (r,n) tales que n=4r+2010².
Para muy avanzados:
-Si f: N--->N, tal que f(f(m)+f(n))=m+n, para todo m, n enteros positivos.
Encontrar todos los posibles valores de f(1988).
Saludos!!
-Encuentra un número de dos dígitos tal que al sumarle 1 y voltear los dígitos del resultado, obtienes un divisor del número.
Para avanzados:
-Encontrar todas las parejas de cuadrados perfectos (r,n) tales que n=4r+2010².
Para muy avanzados:
-Si f: N--->N, tal que f(f(m)+f(n))=m+n, para todo m, n enteros positivos.
Encontrar todos los posibles valores de f(1988).
Saludos!!
Daniel Martínez
viernes, 23 de julio de 2010
Proximos entrenamientos cd. Chihuahua
Los proximos entrenamientos serán los siguientes días:
Sesión #7: Miercoles 4 de Agosto - 9:00-13:00
Sesión #8: Jueves 5 de Agosto - 9:00-13:00
Sesión #9: Viernes 6 de Agosto - 9:00-13:00
Sesión #10: Sabado 7 de Agosto - 9:00-13:00
Sesión #11: Sabado 14 de Agosto - 9:00-13:00
Sesión #12: Sabado 21 de Agosto - 9:00-13:00
En el Tecnologico de Monterrey, edificio de PrepaTec(donde siempre), no hay un salon establecido aun.
Ya queda poco tiempo para el estatal, asi que a prepararse.
Estaremos poniendo problemas aqui en el blog para que resuelvan al menos un problema al dia. Los entrenamientos son importantes, pero tambien lo es el trabajo personal, un problema al dia no les quita casi nada de tiempo y a cambio los hace mejores concursantes y mejores personas. Para los entrenamientos se asumirá que al menos intentaron los problemas bajo el titulo "Problema del dia para novicios".
Sesión #7: Miercoles 4 de Agosto - 9:00-13:00
Sesión #8: Jueves 5 de Agosto - 9:00-13:00
Sesión #9: Viernes 6 de Agosto - 9:00-13:00
Sesión #10: Sabado 7 de Agosto - 9:00-13:00
Sesión #11: Sabado 14 de Agosto - 9:00-13:00
Sesión #12: Sabado 21 de Agosto - 9:00-13:00
En el Tecnologico de Monterrey, edificio de PrepaTec(donde siempre), no hay un salon establecido aun.
Ya queda poco tiempo para el estatal, asi que a prepararse.
Estaremos poniendo problemas aqui en el blog para que resuelvan al menos un problema al dia. Los entrenamientos son importantes, pero tambien lo es el trabajo personal, un problema al dia no les quita casi nada de tiempo y a cambio los hace mejores concursantes y mejores personas. Para los entrenamientos se asumirá que al menos intentaron los problemas bajo el titulo "Problema del dia para novicios".
Isaí Vázquez
jueves, 15 de julio de 2010
Seleccionados Regionales. Cd. Juárez
Lista de seleccionados del examen regional de secundarias de Cd. Juárez 2010.
(la siguiente lista está ordenada alfabéticamente)
América Fernández Sánchez
Berlín Victoria Méndez González
Daniel Antonio Guerrero Lozada
Daniel Chavarría Hernández
Delia Patricia Ponce González
Diana Sofía Hernández Guerrero
Diego Andrés Astiazarán Tobin
Estephania López González
Fernanda Bueno Arango
Francisco Darío Sánchez De la Cruz
Héctor Alejandro García Martínez
Israel Chavarría Hernández
Joana Alejandra Lira Mata
Jorge Iván Díaz Pérez
Laura Idalhi Vargas Rodriguez
Leonardo Isaac Gutiérrez Sierra
Luis David Rincón Loya
Luis Fernando Valdez Caldera
Luis Mauricio Armendáriz Armendáriz
Luis Rodrigo Sánchez López
Manuel Alejandro Navarro Muñoz
María Carolina López Martínez
María Paola Romero Navarro
Mariana Alicia Cruz Medina
Mirka Valeria Méndez González
Mónica Iliana Domínguez De La Torre
Osvaldo Bouche González
Sergio Adrián Ramírez Martínez
Valeria Ileana Saucedo Castro
FELICIDADES!!!
No olviden enviar un correo electrónico de confirmación a esalgado@ommch.org para darles las próximas indicaciones.
martes, 13 de julio de 2010
Problema del dia para novicios
Demostrar que 7|2222^5555 + 5555^2222
sábado, 10 de julio de 2010
Problema del día.
Demostrar que el máximo común divisor de a²+b²-nab y de a+b también divide a n+2.
a y b son enteros positivos.
(a,b)=1
n entera.
Saludos.
a y b son enteros positivos.
(a,b)=1
n entera.
Saludos.
viernes, 9 de julio de 2010
Examen Regional Zona Norte 2010
La Olimpiada Mexicana de Matemáticas en Chihuahua invita a todos los jóvenes que durante el semestre enero-junio de 2010 estuvieron cursando en alguna de las secundarias de la región norte del estado, a participar en el concurso regional de la Olimpiada Mexicana de Matemáticas. Éste se llevará a cabo el día de mañana, sábado 10 de julio, en un horario de 10:00am a 2:30pm, tiempo en el cual tendrán oportunidad de resolver seis problemas matemáticos.
El examen se les aplicará en el edificio G del Instituto de Ingeniería y Tecnología de la UACJ. Se le solicita a todo participante llegar con alrededor de 15 minutos de anticipación para asignarle salón, y a su vez, registrarlo en el concurso. El material necesario es únicamente lápiz, sacapuntas, borrador, bolígrafo (pluma), corrector y juego geométrico (regla y/o escuadra, compás). Por ningún motivo es permitido llevar formulario o apuntes y calculadora a la hora de resolver el examen. Pueden llevar agua, refresco, jugo, fruta, dulces.... si asi se desea, siempre y cuando su consumo no produzca ninguna clase de ruido que resulte molesto para el resto de los participantes, por tal motivo, también se les pedirá apagar por completo sus teléfonos celulares.
Por lo pronto, este examen se aplica SÓLO A JÓVENES DE SECUNDARIA, a los muchachos de preparatoria de la región, se les invita a asistir a los entrenamientos para el concurso estatal, los cuales comienzan el sábado 14 de agosto. El concurso estatal se llevará a cabo el día 28 del mismo mes.
A los asistentes al concurso regional de mañana... les deseamos no suerte, sino ¡ÉXITO!
El examen se les aplicará en el edificio G del Instituto de Ingeniería y Tecnología de la UACJ. Se le solicita a todo participante llegar con alrededor de 15 minutos de anticipación para asignarle salón, y a su vez, registrarlo en el concurso. El material necesario es únicamente lápiz, sacapuntas, borrador, bolígrafo (pluma), corrector y juego geométrico (regla y/o escuadra, compás). Por ningún motivo es permitido llevar formulario o apuntes y calculadora a la hora de resolver el examen. Pueden llevar agua, refresco, jugo, fruta, dulces.... si asi se desea, siempre y cuando su consumo no produzca ninguna clase de ruido que resulte molesto para el resto de los participantes, por tal motivo, también se les pedirá apagar por completo sus teléfonos celulares.
Por lo pronto, este examen se aplica SÓLO A JÓVENES DE SECUNDARIA, a los muchachos de preparatoria de la región, se les invita a asistir a los entrenamientos para el concurso estatal, los cuales comienzan el sábado 14 de agosto. El concurso estatal se llevará a cabo el día 28 del mismo mes.
A los asistentes al concurso regional de mañana... les deseamos no suerte, sino ¡ÉXITO!
jueves, 1 de julio de 2010
Entrenamientos Seleccion Chihuahua
Este verano habrá entrenamientos para todos los seleccionados, las fechas son las siguientes:
Sesión #1: Jueves 8 de Julio 10:00-13:30
Sesión #2: Viernes 9 de Julio 10:00-13:30
Sesión #3: Lunes 12 de Julio 10:00-13:30
Sesión #4: Martes 13 de Julio 10:00-13:30
Sesión #5: Miercoles 14 de Julio 10:00-13:30
Sesión #6: Jueves 15 de Julio 10:00-13:30
Todos los entrenamientos serán en el salón 2104 de PrepaTec (en el edificio donde fue el regional)
La sesion #1 es completamente obligatoria para su participacion en el estatal, ya que se darán instrucciones importantes para los siguientes entrenamientos y para el examen estatal.
Les recuerdo que el examen estatal será el 28 de Agosto en la Universidad Autonoma de Ciudad Juarez. Los entrenamientos, el concurso, y el viaje a Ciudad Juarez son totalmente gratuitos para los seleccionados, asi que no se preocupen por eso.
Cualquier otra cosa no duden en preguntar a mi correo ivazquez@ommch.org
Isaí Vázquez
Edit:
Se cambiaron los entrenamientos del 2104 al 2303
Suscribirse a:
Entradas (Atom)
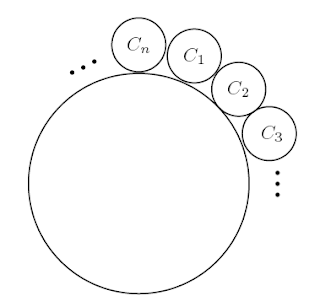





 (Denle click)
(Denle click)