viernes, 31 de diciembre de 2010
Problema del Día (31 de Dic)
Sea $P$ un punto fuera del círculo $C$. Considera todos los trapecios inscritos en $C$ tales que sus lados no paralelos se intersectan en $P$ (al prolongarlos). Muestra que las diagonales de dichos trapecios se intersectan todas en un mismo punto (independientemente del trapecio).
jueves, 30 de diciembre de 2010
Problema del Día (30 de Dic)
Hallar todas las funciones $ f: (0,\infty)\mapsto (0,\infty) $ (es decir, las funciones $f$ de los números reales positivos en los números reales positivos) tales que
\[ \frac{\left( f(w)\right)^{2}+\left( f(x)\right)^{2}}{f(y^{2})+f(z^{2}) }=\frac{w^{2}+x^{2}}{y^{2}+z^{2}} \]
para todos los números reales positivos $ w,x,y,z, $ que satisfacen $wx=yz$
\[ \frac{\left( f(w)\right)^{2}+\left( f(x)\right)^{2}}{f(y^{2})+f(z^{2}) }=\frac{w^{2}+x^{2}}{y^{2}+z^{2}} \]
para todos los números reales positivos $ w,x,y,z, $ que satisfacen $wx=yz$
miércoles, 29 de diciembre de 2010
Problema del Día (29 de Dic)
Sea $A$ un subconjunto de $101$ elementos del conjunto $ S=\{1,2,\ldots,1000000\} $. Prueba que existen números $t_1,t_2, \ldots , t_{100}$ en $S$ tales que los conjuntos
\[ A_{j}=\{x+t_{j}\mid x\in A\},\qquad j=1,2,\ldots,100 \]
son disjuntos por parejas.
\[ A_{j}=\{x+t_{j}\mid x\in A\},\qquad j=1,2,\ldots,100 \]
son disjuntos por parejas.
martes, 28 de diciembre de 2010
Problema del día (28 de Dic)
Determina todas las parejas de enteros $(x,y)$ que cumplen:
\[ 1 + 2^x + 2^{2x+1}= y^2\]
\[ 1 + 2^x + 2^{2x+1}= y^2\]
lunes, 27 de diciembre de 2010
Problema del día (27 de Dic)
Otro IMO reciente de geometría.
Sea $ABC$ un triángulo y sea $I$ el centro de su circunferencia inscrita. Sea $P$ un punto en el interior del triángulo tal que
\[ \angle PBA + \angle PCA = \angle PBC + \angle PCB\]
Demuestre que $AP \geq AI$ y que se da la igualdad si y sólo si $P=I$
Sea $ABC$ un triángulo y sea $I$ el centro de su circunferencia inscrita. Sea $P$ un punto en el interior del triángulo tal que
\[ \angle PBA + \angle PCA = \angle PBC + \angle PCB\]
Demuestre que $AP \geq AI$ y que se da la igualdad si y sólo si $P=I$
domingo, 26 de diciembre de 2010
Problema del día (26 de Dic)
Es día de algebra!
Encuentra todas las funciones $f:\mathbb{R}\rightarrow\mathbb{R}$ tales que para todo $x,y\in\mathbb{R}$ se cumple la siguiente igualdad:
\[ f(\left\lfloor x\right\rfloor y)=f(x)\left\lfloor f(y)\right\rfloor \]
Donde $ \left\lfloor a\right\rfloor $ es la función piso.
Este problema es de una IMO reciente, si ya lo habían hecho me dicen para poner otro.
Encuentra todas las funciones $f:\mathbb{R}\rightarrow\mathbb{R}$ tales que para todo $x,y\in\mathbb{R}$ se cumple la siguiente igualdad:
\[ f(\left\lfloor x\right\rfloor y)=f(x)\left\lfloor f(y)\right\rfloor \]
Donde $ \left\lfloor a\right\rfloor $ es la función piso.
Este problema es de una IMO reciente, si ya lo habían hecho me dicen para poner otro.
sábado, 25 de diciembre de 2010
viernes, 24 de diciembre de 2010
Problema del Día (24 Dic)
Regalito adelantado de navidad de combinatoria.
Se tiene un tablero de 100x100. Cada casilla se pinta de uno de $4$ colores distintos de ta manera que en cada fila y cada columna hay exactamente $25$ casillas de cada color. Demuestra que hay $4$ casillas de colores distintos que forman un rectángulo con lados paralelos al tablero.
Se tiene un tablero de 100x100. Cada casilla se pinta de uno de $4$ colores distintos de ta manera que en cada fila y cada columna hay exactamente $25$ casillas de cada color. Demuestra que hay $4$ casillas de colores distintos que forman un rectángulo con lados paralelos al tablero.
jueves, 23 de diciembre de 2010
Problema 4 del nacional XXII (San Carlos 2008)
Este problema es uno de los 4 más difíciles que recuerdo. No me ha salido, otro 4 difícil es el 4 de Oaxtepec 2001 (OMM XV), pero ese me sale cada vez que lo intento porque ya me acuerdo del truquito.
Problem 4 OMM XII:
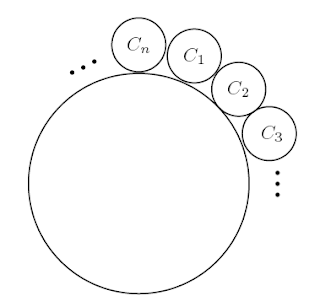
Los caballeros $ C_1,C_2,\ldots,C_n $, del Rey Arturo, se sientan en una mesa
redonda de la siguiente manera:
El rey decide realizar un juego para premiar a uno de sus caballeros. Iniciando con $ C_1 $, y avanzando en el sentido de las manecillas del reloj, los caballeros irán diciendo los números 1, 2, 3, luego 1, 2, 3, y así sucesivamente (cada caballero dice un número). Cada caballero que diga 2 ó 3 se levanta inmediatamente y el juego continúa hasta que queda un solo caballero: el ganador.
Por ejemplo, si $ n = 7 $, los caballeros dirán 1, 2, 3, 1, 2, 3, 1 en la primera vuelta; después $ C_1 $ dirá 2 y $ C_4 $ dirá 3, y gana entonces el caballero $ C_7 $.
Encuentra todos los valores de $ n $ de tal manera que el ganador sea el caballero $ C_{2008} $.
Problem 4 OMM XII:
Los caballeros $ C_1,C_2,\ldots,C_n $, del Rey Arturo, se sientan en una mesa
redonda de la siguiente manera:
El rey decide realizar un juego para premiar a uno de sus caballeros. Iniciando con $ C_1 $, y avanzando en el sentido de las manecillas del reloj, los caballeros irán diciendo los números 1, 2, 3, luego 1, 2, 3, y así sucesivamente (cada caballero dice un número). Cada caballero que diga 2 ó 3 se levanta inmediatamente y el juego continúa hasta que queda un solo caballero: el ganador.
Por ejemplo, si $ n = 7 $, los caballeros dirán 1, 2, 3, 1, 2, 3, 1 en la primera vuelta; después $ C_1 $ dirá 2 y $ C_4 $ dirá 3, y gana entonces el caballero $ C_7 $.
Encuentra todos los valores de $ n $ de tal manera que el ganador sea el caballero $ C_{2008} $.
Solucion P6 OMM 24
Para los que todavia no saben como se hace el 6 :P
Este es el primer nacional en que se como se hacen los 6 problemas.
Del 2008 no se como hacer el 3,4,5 y del 2009 el 2 y 6
Lo hice ayer en la noche
Esta en un comentario porque esta poco largo.
Este es el primer nacional en que se como se hacen los 6 problemas.
Del 2008 no se como hacer el 3,4,5 y del 2009 el 2 y 6
Lo hice ayer en la noche
Esta en un comentario porque esta poco largo.
Problema del día (23 dic)
Ahora toca números:
Encuentra todas las parejas $(n,m)$ de enteros tales que $2^n+3^m$ es un cuadrado perfecto.
Encuentra todas las parejas $(n,m)$ de enteros tales que $2^n+3^m$ es un cuadrado perfecto.
miércoles, 22 de diciembre de 2010
Problema del Dia (22 Dic)
Vuelve el problema del día al blog. Los problemas que se estarán poniendo serán de nivel avanzado, es decir nacionales dificiles, IMOs faciles y por el estilo.
Los objetivos de esta temporada del problema del día son basicamente apoyar a Karina en su trayecto a la IMO, apoyar a Alberto para que le valla bien en los entrenamientos nacionales y en el proximo nacional y darle algo que hacer a los olimpicos repetidores y entrenadores que se aburren (nos aburrimos) en estas vacaciones de invierno.
Comenzaremos con un problema de geometria de una IMO reciente.
Un triángulo acutángulo $ABC$ tiene ortocentro $H$. La circunferencia con centro en el punto medio de $BC$ que pasa por $H$ corta a la recta $BC$ en $A_1$ y $A_2$. La circunferencia con centro en el punto medio de $CA$ que pasa por $H$ corta a la recta $CA$ en $B_1$ y $B_2$. La circunferencia con centro en el punto medio de $AB$ que pasa por $H$ corta a la recta $AB$ en $C_1$ y $C_2$. Demostrar que $A_1,A_2,B_1,B_2,C_1,C_2$ están sobre una misma circunferencia.
Si a la semana nadie ha resuelto un problema, pongo sugerencia.
Los objetivos de esta temporada del problema del día son basicamente apoyar a Karina en su trayecto a la IMO, apoyar a Alberto para que le valla bien en los entrenamientos nacionales y en el proximo nacional y darle algo que hacer a los olimpicos repetidores y entrenadores que se aburren (nos aburrimos) en estas vacaciones de invierno.
Comenzaremos con un problema de geometria de una IMO reciente.
Un triángulo acutángulo $ABC$ tiene ortocentro $H$. La circunferencia con centro en el punto medio de $BC$ que pasa por $H$ corta a la recta $BC$ en $A_1$ y $A_2$. La circunferencia con centro en el punto medio de $CA$ que pasa por $H$ corta a la recta $CA$ en $B_1$ y $B_2$. La circunferencia con centro en el punto medio de $AB$ que pasa por $H$ corta a la recta $AB$ en $C_1$ y $C_2$. Demostrar que $A_1,A_2,B_1,B_2,C_1,C_2$ están sobre una misma circunferencia.
Si a la semana nadie ha resuelto un problema, pongo sugerencia.
lunes, 20 de diciembre de 2010
Examenes de entrenamiento 1 y 2
PRIMER EXAMEN DE ENTRENAMIENTO
Problema 1.
Muestra que 2010 no se puede escribir como una diferencia de dos cuadrados.
Problema 2.
Sea $ABC$ un triángulo y $D$ un punto sobre el lado $BC$. Sean $U$ el circuncentro del triángulo $BDA$ y $V$ el circuncentro del triangulo $CDA$.
Muestra que $ABC$ y $AUV$ son semejantes.
Problema 3.
Sean $a,b$ numeros reales con $0 \leq a , b \leq 1$. Muestra la desigualdad:
\[ \sqrt{a^3 b^3} + \sqrt{(1-a^2)(1-ab)(1-b^2)} \leq 1 \]
Cuando ocurre la igualdad?
Problema 4.
Una sucesion {$a_n$} con $a_n = a + nd$ se conoce como una $progresion$$aritmetica$. La sucesion {$b_n$} donde $b_n = \sum_{i=0}^{n} a_i$se conoce como una $progresion$$aritmetica$$de$$segundo$$grado$.
Considera todas las progresiones aritmeticas {$a_n$} que cumplan que $a$ y $d$ son enteros positivos y tales que su progresion aritmetica de segundo grado {$b_n$} contiene al numero 2010.
$(a)$ Cual es el mayor indice $n$ que cumple con $b_n = 2010$ ?
$(b)$ Encuentra todas las progresiones aritmeticas {$a_n$} para las que $b_n = 2010$ para el indice $n$ de la parte $(a)$.
SEGUNDO EXAMEN DE ENTRENAMIENTO
Problema 1.
Considera $M_n =$ {$0, 1, 2, \ldots , n$} el conjunto de los enteros no-negativos menores o iguales a $n$. Un subconjunto $K$ de $M_n$ se dira $"regulado"$ si no es vacio y para cada $k \in K$ existe un subconjunto $L$ de $K$ con exactamente $k$ elementos.
Cuantos subconjuntos regulados hay en $M_n$ ?
Problema 2.
Para $n \geq 1$ natural considera a $f(n) = 1 + n + n^2 + \ldots + n^{2010}$ .
Muestra que ningún entero del conjunto {$2, 3, 4, \ldots , 2010$} divide a $f(n)$,
Problema 3.
Una diagonal de un hexagono convexo se dira $"diagonal$$mayor"$, si divide al hexagono en dos cuadrilateros. Dos diagonales mayores dividen al hexagono en dos triangulos y en dos cuadrilateros.
Un hexagono convexo $H$ tiene la propiedad de que cada division de $H$ por dos de sus tres diagonales mayores siempre tiene los dos triangulos isosceles y con lados del hexagono como bases.
Muestra que los vertices de $H$ estan sobre una circunferencia.
Problema 4.
Dos disecciones de un cuadrado en tres rectangulos se consideran iguales si una se puede obtener de la otra por un reacomodo de las tres piezas (para formar el cuadrado).
Cuantas disecciones diferentes hay de un cuadrado de lado 2010 en tres rectangulos, si los rectangulos tienen lados de longitudes enteras y el area de un rectangulo es igual a la media aritmetica de las areas de los otros dos?
Problema 1.
Muestra que 2010 no se puede escribir como una diferencia de dos cuadrados.
Problema 2.
Sea $ABC$ un triángulo y $D$ un punto sobre el lado $BC$. Sean $U$ el circuncentro del triángulo $BDA$ y $V$ el circuncentro del triangulo $CDA$.
Muestra que $ABC$ y $AUV$ son semejantes.
Problema 3.
Sean $a,b$ numeros reales con $0 \leq a , b \leq 1$. Muestra la desigualdad:
\[ \sqrt{a^3 b^3} + \sqrt{(1-a^2)(1-ab)(1-b^2)} \leq 1 \]
Cuando ocurre la igualdad?
Problema 4.
Una sucesion {$a_n$} con $a_n = a + nd$ se conoce como una $progresion$$aritmetica$. La sucesion {$b_n$} donde $b_n = \sum_{i=0}^{n} a_i$se conoce como una $progresion$$aritmetica$$de$$segundo$$grado$.
Considera todas las progresiones aritmeticas {$a_n$} que cumplan que $a$ y $d$ son enteros positivos y tales que su progresion aritmetica de segundo grado {$b_n$} contiene al numero 2010.
$(a)$ Cual es el mayor indice $n$ que cumple con $b_n = 2010$ ?
$(b)$ Encuentra todas las progresiones aritmeticas {$a_n$} para las que $b_n = 2010$ para el indice $n$ de la parte $(a)$.
SEGUNDO EXAMEN DE ENTRENAMIENTO
Problema 1.
Considera $M_n =$ {$0, 1, 2, \ldots , n$} el conjunto de los enteros no-negativos menores o iguales a $n$. Un subconjunto $K$ de $M_n$ se dira $"regulado"$ si no es vacio y para cada $k \in K$ existe un subconjunto $L$ de $K$ con exactamente $k$ elementos.
Cuantos subconjuntos regulados hay en $M_n$ ?
Problema 2.
Para $n \geq 1$ natural considera a $f(n) = 1 + n + n^2 + \ldots + n^{2010}$ .
Muestra que ningún entero del conjunto {$2, 3, 4, \ldots , 2010$} divide a $f(n)$,
Problema 3.
Una diagonal de un hexagono convexo se dira $"diagonal$$mayor"$, si divide al hexagono en dos cuadrilateros. Dos diagonales mayores dividen al hexagono en dos triangulos y en dos cuadrilateros.
Un hexagono convexo $H$ tiene la propiedad de que cada division de $H$ por dos de sus tres diagonales mayores siempre tiene los dos triangulos isosceles y con lados del hexagono como bases.
Muestra que los vertices de $H$ estan sobre una circunferencia.
Problema 4.
Dos disecciones de un cuadrado en tres rectangulos se consideran iguales si una se puede obtener de la otra por un reacomodo de las tres piezas (para formar el cuadrado).
Cuantas disecciones diferentes hay de un cuadrado de lado 2010 en tres rectangulos, si los rectangulos tienen lados de longitudes enteras y el area de un rectangulo es igual a la media aritmetica de las areas de los otros dos?
Suscribirse a:
Entradas (Atom)